IntMath Newsletter: Math carnival, new interactives, graphing letters
By Murray Bourne, 11 Sep 2014
11 Sep 2014
In this Newsletter:
1. Carnival of Mathematics #114
2. Updated Graphs of tan, cot, sec and csc
3. Graphing letter distribution
4. Math puzzles
5. Final thought - The skill of asking questions
1. Carnival of Mathematics #114
It was my turn to host the 114th Math blog Carnival. I hope you find something interesting in the 16 articles there!
 |
The Carnival of Mathematics is a collection of recent math blog articles covering visual math, various rants and some math history, by various authors. See: |
2. Updated Graphs of tan, cot, sec and csc
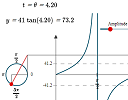 |
The updated applets on the Graphs of tan, cot, sec and csc page now run on mobile devices, albeit rather slowly. This leads to one of the most popular pages on IntMath. |
3. Graphing letter distribution
We live in a great age where it's possible to see a lot more in data that was ever possible before computers.
Prooffreader (by David Taylor) has some interesting data visualizations, including several displaying trends in baby names. The name "Shirley" sky-rocketed in the mid-1930s, and "Linda" even more so in the the late 1940s. "Brittany" and "Ashley" were hits in the late 1980s. There's an interesting animation of the rapid rise in boy's names ending in "n".
He also has some infographics on cancer and mortality rates.
One of the graphics that caught my eye was Graphing the Distribution of English, which demonstrates how letters are used in words in the English language.
For example, the image below for the first 2 letters indicates that "a" occurs mostly in the middle of a word, whereas "b" occurs mostly at the beginning.
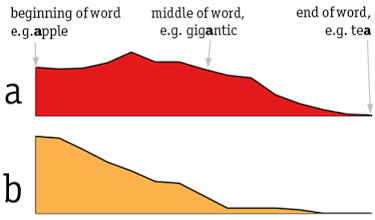
Go check out Prooffreader - there are some interesting things there.
4. Math puzzles
The puzzle in the last IntMath Newsletter asked about a strange pyramid of ancient Egypt. The correct answer with explanation was given by Tomas and Nicos. The difference in their approaches was quite interesting.
New math puzzle: Find the smallest rectangle (non-square and with integer sides) where the perimeter equals the area (ignoring units).
Leave your responses here.
5. Final thought - the skill of asking questions
This quote comes from Annie Murphy Paul. It's a summary of the Rothstein and Santana book, Make Just One Change: Teach Students To Ask Their Own Questions:
"This book makes two simple arguments: 1) All students should learn how to formulate their own questions. 2) All teachers can easily teach this skill as part of their regular practice. This inspiration for the first argument came from an unusual source. Parents in the low-income community of Lawrence, Massachusetts, with whom we were working twenty years ago told us that they did not participate in their children's education nor go to their children's schools because they 'didn't even know what to ask.' It turns out that they were actually pointing to a glaring omission in most formal and informal educational enterprises. The skill of being able to generate a wide range of questions and strategize about how to use them effectively is rarely, if ever, deliberately taught. In fact, it has too often been limited to students who have access to an elite education. Our goal is to democratize this teaching of an essential thinking and learning skill that is also an essential democratic skill."
—Dan Rothstein and Luz Santana, Make Just One Change: Teach Students To Ask Their Own Questions
Until next time, enjoy whatever you learn.
See the 16 Comments below.
11 Sep 2014 at 7:07 pm [Comment permalink]
smallest sides of rectangle: 6 and 3
11 Sep 2014 at 8:19 pm [Comment permalink]
Puzzle Answer
Perimeter equals area so
2A + 2B = AB
Solving for one of the dimensions
AB - 2A = 2B
A(B - 2) = 2B
A = 2B/(B-2) The smallest number for B that results in a positive integer value is B = 3 which generates A = 6
2(6) + 2(3) = 18 = (6)(3)
11 Sep 2014 at 10:22 pm [Comment permalink]
The smallest rectangle (non-square and with integer sides) where the perimeter equals the area would be a 3 X 6 rectangle:
Since the perimeter and area of the rectangle are the same value, I let the short side = x and the long side = y, and
then 2x + 2y = xy
Solving for x gives x = (-2y)/(2-y).
Since the sides must be integers, and x cannot equal y, the smallest result possible is when x = 6 and y = 3.
12 Sep 2014 at 1:42 am [Comment permalink]
Make a table, using small integers until the perimeter no longer exceeds the area. Equality occurs with a 3x6 rectangle.
12 Sep 2014 at 2:17 am [Comment permalink]
Let a be the height and a + j the base of the rectangle, where both a and j are integers. Then the condition that the perimeter and the area are equal (ignoring the units, for the area is in terms of the square units of the parameter's) is given by
2 a + 2 (a + j) = a (a + j).
A straightforward way to examine the problem is to determine if this condition is satisfied for integer values of a and j, both ranging, say, from 1 to 50.
The only case which satisfies the condition in this range is when a = 3 and j = 3, i.e., base = 6 and height = 3. Any other solution would have both its sides larger than 50.
12 Sep 2014 at 4:45 am [Comment permalink]
Let x the length and y the width of the rectangular. The area is E=xy and the perimeter is P=2(x+y). Due to E=P (only in arithmetical value), xy=2(x+y) => y=2x/(x-2). The positive curve of the Function F(x)=2x/(x-2) represents all the pairs (x,y) which are the solutions of F(x) in R-{2}. The curve is symmetrical to the axis y=x and its peak is where the axis intersects the curve. Or, else, the point where the line tan(135 deg) tangents to the curve, which is the Derivative of the Function at that point: tan(135deg) = F'(x) => -1=-4/(x-2)^2 => x=4. So, the solution is the pair (4,4), but it is a square. The nearest integers are 3, 5, 6. For x=5, y=10/3 which is not an integer. According to the problem, the acceptable solutions are x=3, y=6 or x=6, y=3. When x->2 then limF(x)->inf. and the area is gradually being augmented. The lines x=2 and y=2 are asymptotical to the curve F(x). While x tends towards 4 the area is diminishing.
12 Sep 2014 at 5:10 am [Comment permalink]
Answer to the puzzle:
2a+2b = ab
b = 2a/(a-2)
This is the graph of a hyperbola, where a=2 is a vertical asymptote.
Drawing the graph, integer pairs are (4,4) square; (0,0) nothing; (-2,1) one side not >0; and (6,3).
Therefore, (6,3) is the smallest non-square integer pair. In fact is it the only pair.
12 Sep 2014 at 5:32 pm [Comment permalink]
The smallest possible rectangle is of sides 6 units by 3 units
Solution:
If l is the length and b is the breadth,
area = perimeter, numerically
implies lb = 2(l+b)
implies l= 2b/b-2
implies b-2 =1
implies b=3, so l= 6
12 Sep 2014 at 8:12 pm [Comment permalink]
Perimeter=x*y
Area=2*x+2*y
Then:x*y=2*x+2*y
Thus x*y-2*y=y and y=2*x (x and y are integers)
x-2=1
x=3 and y=6
Sorry,I don^t speack English.Only I can read it.
It^s the first time I write You.
I hope You understand Me.
I think You are a Big man
Thank You
14 Sep 2014 at 12:34 am [Comment permalink]
solution :
Area= 3x6=18
perimeter = 2(3+6)=18
therefor the only solution for a rectangle is one side 3 any other side is 6.
we notice that if it is a square the side will be 4 and the area will be 16 and the perimeter will be 16.
to solve the problem let b > a and let b=na , were n is and integer
the area will be a squared b and the perimeter is 2(a+na) = 2a(1+n)
we notice that this to be true for integers only divisor should be even and in this case should be equal to
two or one and in the case of one we get the square and in the case of two tree and six for the side of the rectangle.
this is a concise solution.
14 Sep 2014 at 10:25 am [Comment permalink]
Mr Bourne.
In my past answer, the smallest rectangle has two sides of
3u and two sides of 6u.Let: x=3 and y=6
From x*y=2*x+2*y
y=(2*x)/(x-2)
y>=1 and x>=1
Then I^ve got:x is not equal 1 because of y is not equal -2
Besides x can not equal 2.
Is this a proof?
Best regards,Francisco
15 Sep 2014 at 12:27 pm [Comment permalink]
My answer would be 3 units by 6 units.
The perimeter = 2(3 + 6) or 18 units.
The area = 3 * 6 or 18 square units.
18 Sep 2014 at 1:20 am [Comment permalink]
The answer is 18 but I cannot see how to solve the equation xy = 2x + 2y for minimum values of x and y.
30 Sep 2014 at 1:15 pm [Comment permalink]
This is an old problem. Finding 2 d shapes whose perimeter is numerically equal to their area. One naturally can extend this problem to find 3 d shapes whose surface area us numerically equal to their volume. PROBLEM IS CALLED EQUABLE SHAPES.
NOW as far as solving xy=2x+2y is concerned:
1. Rearrange to make y subject thus:
xy-2y=2x
2. Factorise
y(x-2)=2x
3. So y=2x/(x-2)
4. Treating x as the independent variable and y as dependent
One can choose values for X and generate values for y and naturally graph this
5. Graph this and from graph there are an infinite number of solutions
(4,4) square is rect whose length is its width
(3,6) , (6,3).
(5, 10/3) etc
nice problem when try this on as many 2 d and 3 d shapes as one feels.
i have a problem to share with anyone with an interest in maths.
As i dont say math but maths i hope people will deduce that maybe I am probably from the u.k.
i have previously posted this on the Internet and no one besides myself solved it.
I AM THROWING IT OUT THERE AGAIN FOR SOMEONE TO PLAY WITH.
ANYONE INTERESTED THEN EMAIL ME AND I WILL SEND THE REFERENCE OR STATE THE PROBLEM FORMERLY
25 Nov 2014 at 6:27 am [Comment permalink]
I've lost a couple back issues of this newsletter. What's the procedure for recovery?
25 Nov 2014 at 8:21 am [Comment permalink]
Hi Michael
Recent IntMath Newsletters can be found here:
IntMath Newsletters archive
The whole lot are listed here:
sitemap.
Thanks for your interest!