Carnival of Mathematics 114

Helix Bridge and Flyer, Singapore

114 is a sphenic number (the product of 3 distinct prime numbers):

114 = 2 × 3 × 19

It's also a repdigit: 114 = 222₇ (the digits repeat in the base 7 representation)

It's the 19th number in the Padovan sequence, given by the recurrence relation P(n) = P(n − 2) + P(n − 3), and where the first 3 terms are 1.

114 is an abundant number (where the sum of its proper divisors is greater than itself):

1 + 2 + 3 + 6 + 19 + 38 + 57 > 114

That's appropriate, as we have abundant posts for this, the 114th Carnival of Mathematics!

On with the show.

1. Visual math

a. The Spellbinding Mathematical GIFs Of Dave Whyte

Now here are some animations that could be the basis for some interesting class discussion. See The Spellbinding Mathematical GIFs Of Dave Whyte

b. 6th meeting on Origami, Science, Math, and Education

Andrea Hawksley gives us a nice roundup of the recent meeting on Origami, Science Math and Educaion. She features some of her own work, as well as other gems that were presented. See:

6th meeting on Origami, Science, Math, and Education (6OSME)

While you're there, mouse over Andrea's name in the header of her blog. It's cute.

c. Random Walks Mural

Mike Chase of "Walking Randomly" tells us about producing three 2-dimensional random walks on the back wall of his classroom. There is a video documentary with time lapse footage, and a discussion of some of the math questions that arise when thinking about random walks.

That's logical, as it's the name of his blog! See

Random Walks Mural

2. Rants

a. BBC Sport's Anti-Smartness Bias

Colin Beveridge of "Flying Colours Maths" rants against what is all-too common in the media: laughing at the nerds. He argues the case that if we want a culture where science and maths are seen as important things to study, we might start by making sure people who study them aren’t criticised for it.

See:

BBC Sport's Anti-Smartness Bias

b. The science at the end of the Whoniverse

In a similar vein, Gilead of "Tycho's Nose" rants about inaccuracies (or part-truths) in background equations as seen in the new Doctor Who series. See: The science at the end of the Whoniverse

c. Stem and Leaf – is there a point?

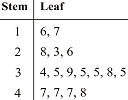Here's a rant of a different nature. Stephen Cavadino of "cavmaths" questions whether stem-and-leaf plots are a necessary part of the math curriculum. See: Stem and Leaf – is there a point?

3. Exploring math ideas

a. When do n and 2n have the same digits? 

Mark Dominus provides us with a neat exploration of numbers that are permutations of each other. His first example is the decimal expansion of n/7.

See:

When do n and 2n have the same digits?

b. The Revenge of the Perko Pair

Richard Elwes introduces us to an interesting knotty problem. It turns out this generally accepted picture is wrong... See how at: The Revenge of the Perko Pair

c. Looking for Life

Antonio Sánchez Chinchón presents an R implementation of Conway's Game of Life, a cellular automaton that could support universal computation. He looks for periodic objects able to do computations in the Game Of Life. See Looking for Life [no longer available]

d. When Greedy Algorithms are Perfect: the Matroid

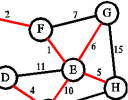Jeremy Kun of "Math ∩ Programming" explores optimal greedy algorithms and matroids.

See:

When Greedy Algorithms are Perfect: the Matroid

e. Arc length of a spiral around a paraboloid

This post, right here on "squareCircleZ", was inspired by a reader's question. He makes solar cookers for use in Africa and wanted to know how to construct the spiral length around his cookers. It's some "real-world" math that involves sustainable, cheap energy.

See:

Arc length of a spiral around a paraboloid

5. Math history

a. Look Ma, No Zero

0	In a lot to do about nothing, Evelyn Lamb of the Scientific American blog, recounts her journey of discovery with her students, which involved decipering Plimpton, the 4000 year-old Babylonian tablet.

So how did the Babylonians work in base 60, without 0 as a place holder?

See:

Look Ma, No Zero

b. How The Ancient Egyptians (Should Have) Built The Pyramids

So, how did the ancient Egyptians move those 2.4 million blocks, weighing up to 80 tonnes? In this Physics arXiv post, we learn: Modifying square blocks to form dodecagons would have made them easy to roll, say physicists.

See:

How The Ancient Egyptians (Should Have) Built The Pyramids

6. Plug

This post is a plug for an experimental MOOC (Massive Open Online Course). The blurb says:

"Citizen Maths is an online resource anyone can use — to discover how maths can be a powerful tool for solving those problems that come up at work and in your life."

See:

Citizen Maths MOOC

7. Reflections

So, what is mathematics? Shecky Riemann of "Math-Frolic" has a quote from How Mathematicians Think, by William Byers, which ponders that math is a series of situations where we are led to observe,

"Something's Going On Here"

8. Final bit

I hope you've enjoyed Mathematics Carnival #114, coming to you from Singapore.

The next carnival will be at MathTuition88, slated for October 2014. See where and how to submit.

Image credits:

Singapore Helix and Flyer by ensogo, accessed from http://www.ensogo.com.ph/escapes/singapore-flyer-cruise-09092012.html

BBC Sport logo, by BBC, accessed from http://www.bbc.com/sport/0/

Stem & leaf plot by ck-12.org, accessed from http://www.ck12.org/book/Basic-Probability-and-Statistics-A-Full-Course/r4/section/7.2/

Reflection, by Marcia Birken, accessed from http://alumnae.mtholyoke.edu/blog/light-motifs-marcia-birkens-images-meld-math-and-art/

All other images are from the posts to which they link. If you have any objections to their use in this manner, let me know and I'll remove them.

See the 5 Comments below.