Archimedes and the area of a parabolic segment
By Murray Bourne, 14 Dec 2008
Archimedes was a Greek mathematician who lived 2300 years ago.
Many of his inventions and mathematical discoveries were years ahead of their time. It's amazing how inventive you become when you are constantly under attack from your enemies.
Finding the area under a curve had been a problem for many years. Fair trade depended (in part) on being able to work out volumes of cylinders and spheres. Archimedes worked out good approximations for the area of a circle and the value of π (pi).
The most remarkable thing about the following example of Archimedes' thinking is that it pre-dates the work of Isaac Newton and Gottfried Leibniz (the 17th century mathematicians who developed differential calculus) by around 2000 years.
I have a special interest in this kind of thing because the name of this blog, squareCircleZ, is derived from the historical attempt to construct a square with the same area as a given circle (called "squaring the circle").
The following discussion follows the technique as outlined by Archimedes in his Quadrature of the Parabola, using the "method of exhaustion", a pre-cursor to infinitesimal calculus. The concept came via Antiphon (5th century BCE), and Eudoxus of Cnidus (4th century BCE).
The area of a parabolic segment
A parabolic segment is a region bounded by a parabola and a line, as indicated by the light blue region below:
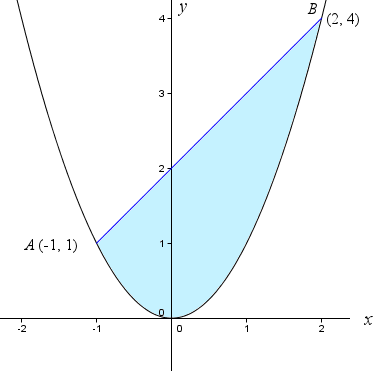
[See Parabola for some background on this interesting shape.]
I have used the simple parabola y = x2 and chosen the end points of the line as A (−1, 1) and B (2, 4). The theorem will work for any parabola and any line passing through that parabola, intersecting in 2 points. [Of course, Archimedes did not use the x-y co-ordinate system, since it was not invented by Descartes until the 17th century.]
Archimedes then located point C such that the x-value of C is half-way between the x-values of points A and B. He then constructed triangle ABC, as follows:
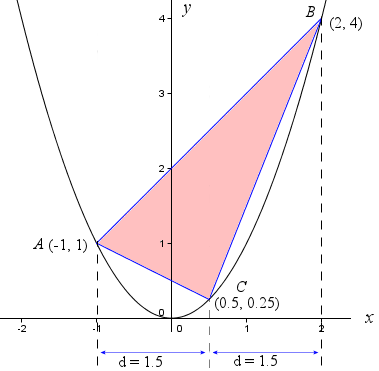
In my example, C has x-value 0.5, which is 1.5 units from both x = −1 and x = 2.
Archimedes showed that the area of the (light blue) parabolic segment is 4/3 of the area of the triangle ABC.
The way Archimedes achieved this result was to use the Method of Exhaustion, which involves finding the area of a curved shape by inscribing successively smaller polygons until the shape is filled. We can find the area of those polygons and hence the area of the curved shape.
We now construct another triangle by choosing point D on the parabola such that its x-value is half-way between the x-values of A and C, similar to what we did before.
Let's zoom in and see the result.
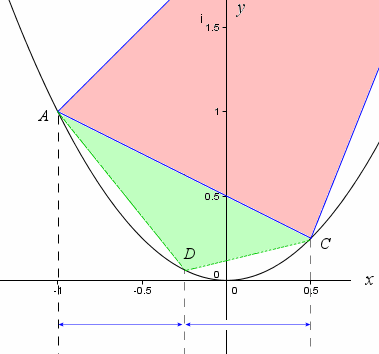
We do the same thing on line BC, by locating point E such that its x-value is half-way between C and B.
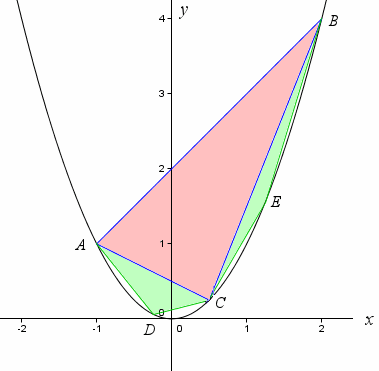
We can see already that if we add the areas of triangles ABC, ACD and BCE, we have a reasonable approximation for the area of the parabolic segment, but we can do better.
If we continue the process, we form 4 more triangles as follows:
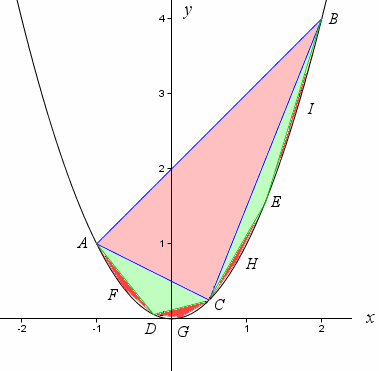
There is very little 'white space' left and if we were to add the areas of the 7 triangles, we would have an even better approximation for the area of the parabolic segment.
If we kept going and added the areas of an infinite number of such triangles, we would have an exact area for the parabolic segment.
Now, the area of each light green triangle is 1/8 the area of the pink triangle. This is because the green triangle has 1/2 the width of the pink triangle (we made it so) and 1/4 of the height (which can be shown using parametric equations.)
Then, considering the red triangles, they will be 1/8 the area of the light green triangles.
So if we call the area of the large pink triangle X, then the area of all of the triangles is given by:
X + 2(X/8) + 4(X/64) + 8(X/512) + ...
= X + X/4 + X/16 + X/64 + ...
= X(1 + 1/4 + 1/16 + 1/64 + ...)
We recognize that the expression in brackets is a Geometric Series, with common ratio r = 1/4 and first term a = 1. The sum of this series is given by:
Sum = a/(1 − r) = 1/(1 − 1/4) = 1/(3/4) = 4/3
[Archimedes used a geometric proof for this portion.]
So the total area of the triangles (which gives us the area of our light blue parabolic segment) is 4X/3, which is 4/3 the area of the pink triangle, as Archimedes claimed.
The thinking behind this solution is very similar to the ideas behind the development of calculus.
Using Calculus
Let's use integral calculus to check the answer we obtained using Archimedes' approach.
In my particular example, with y = x2 and the line y = x + 2 intersecting the parabola at (−1, 1) and (2, 4), the pink triangle has width AC = 1.68 units and perpendicular height 4.02 units, so the area is:
Area ΔABC = 0.5 × 1.68 × 4.02 = 3.38 unit2
So according to Archimedes, the area of the (light blue) parabolic segment will be:
Area segment = 4/3 × 3.38 = 4.5 unit2
Now, let's compare this result using calculus. The required area is an area between 2 curves. The upper curve is the line y2 = x + 2 and the lower curve is y1 = x2. The limits of integration are x = −1 and x = 2.
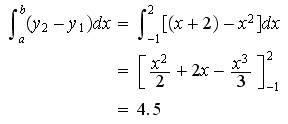
So we get the same answer, 4.5 unit2.
As I said at the beginning, Archimedes' solution for finding the area of a parabolic segment is a remarkable result. Almost 2000 years before Newton and Leibniz formalized differential and integral calculus, Archimedes already had a good handle on the basics.
It's interesting (and dangerous) how knowledge can be 'forgotten' for thousands of years.
Go here to see an interesting English translation of Archimedes' Quadrature of the Parabola.
The graphs in this article were produced using Geogebra, the free computer algebra system. See my review: GeoGebra math software - a review.
See the 26 Comments below.

16 Dec 2008 at 2:43 pm [Comment permalink]
a very wonderful archimedes. he's very brilliant
16 Dec 2008 at 4:59 pm [Comment permalink]
An Easier Way?
If we lay a string along the outline of the blue area, then divide the length of the string by 4, we get the side of a square. Simply squaring this distance gives us the area.
If an easier way can be used in some situations, shouldn't we use it?
16 Dec 2008 at 5:24 pm [Comment permalink]
Nevermind, I read further and found that it was reduced to 4X/3.
Clearly easier once the initial math is formed.
16 Dec 2008 at 8:33 pm [Comment permalink]
Hi Mick
Your "easier way" suggestion intrigued me.
The length of the curved part (the parabola) will be close to 6.1 units. I didn't use string, I used the formula for the length of a curve:
And in our particular case:
The length of the straight edge of the blue segment is around 4.2 units (once again, no strings on me - I used the distance formula).
So the total distance around the blue segment is about 10.3 units. Divide this by 4 and you get 2.575. Square this and you get 6.63 square units.
So this approach kinda inflates the actual area (4.5 sq units) somewhat.
I went through this because I totally agree that "If an easier way can be used in some situations, shouldn't we use it?"
17 Dec 2008 at 2:10 am [Comment permalink]
Mick, that is definitely an interesting way to look at the problem. While I also agree that the faster way to obtain an answer should be used, let us look at another case.
Let's take two geometric shapes that have the same known area. and that we know a formula to find the area and perimeter.
For arguments sake, let's look at a square with dimensions 10x10, and a rectangle with dimensions 50x2.
Both shapes have an area of 100 sq. units, but if we look at the perimeters of both, the square is 40 units, and the rectangle is 102 units.
You can probably see where this is going, if we divide 102 by 4 we get 25.2 and if we square this value then our estimated area is 650.25 sq. units rather than the actual value of 100 sq units.
Although this seemed to have worked better in the case above, it wouldn't work universally. Great way of thinking outside the box though!
Happy Holidays,
mr. smith
19 Dec 2008 at 1:42 am [Comment permalink]
Its pretty amazing that Archimedes already discovered calculus that long ago. It's pretty similar to the Mayan advances in astronomy and other arts centuries before Europe ever even began using it.
30 Apr 2009 at 7:11 pm [Comment permalink]
I didnt understand how the area of the green triangles can be equal to 1/8 area of big one..
1 May 2009 at 3:12 pm [Comment permalink]
Lakshman. The best way to see this is to go ahead and calculate the area of the pink and (one of the) green triangles. You could use the bounding box method, too.
4 Apr 2010 at 6:32 pm [Comment permalink]
this is gud and an amazing task done by u!
but u can add more relevant details concerning the same topic!
pls add more examples!
9 Jan 2011 at 6:22 pm [Comment permalink]
Thank you very much for putting this up. It's very well done.
19 Jun 2011 at 7:06 pm [Comment permalink]
it's really nice,thank you!!!
29 Jun 2011 at 7:47 pm [Comment permalink]
It very easy nd nice of him, u really make evry thing easy 4 me especially. I wish i am a genius lyk him
23 Aug 2011 at 3:01 pm [Comment permalink]
nose bleed!!! but nice thanks.... am learning a lot, it's help me a lot 2 my work!!!!
1 Dec 2011 at 10:21 am [Comment permalink]
It is very interesting to see how Archimedes arrived at the area of curved segments as above. But what intrigues me, with out co-ordinate geometry at his disposal, what was his definition of the Parabola and how he chose points on the curve !!!!
23 Feb 2012 at 4:23 pm [Comment permalink]
The height and width of the pink triangle are 3 and 2.25. How have these been found?
5 Mar 2012 at 7:29 pm [Comment permalink]
@Owain: I (easily) found the dimensions using GeoGebra. I revised that portion to make it a bit clearer what I'm doing. Hope it helps.
27 Apr 2012 at 7:33 pm [Comment permalink]
Archimedes was a great mathematician; one of the three greatest (along with Newton and Gauss). But he did not invent Differential Calculus. At best, he foresaw, the development of limits and integrals - this is what your blog shows. There remain derivatives and the Fundamental Theorem of Calculus, not to mention continuity that was developed in the 19th century.
27 Apr 2012 at 10:41 pm [Comment permalink]
Yes, Alexander. My <140-character tweet missed much of your more accurate summary!
2 Jun 2012 at 5:40 pm [Comment permalink]
Hi! I wonder, how did you think out that the width was 1/2 of the pink triangle and the height 1/4 of the pink triangle? Could you show me? I have an assignment where I have to show that this method is working generally, without any x-values.
Thankful for a quick response!
4 Jun 2012 at 7:20 pm [Comment permalink]
Hi Johan
There's a few ways you can go about this.
As I mentioned in the article, you can use parametric equations to demonstrate the comparative heights (it's probably easier to use one actual point on the curve, say (-1,1) and another general point (t, t2).
Another approach is to notice there are common edges for the pink triangle and the green triangles. This makes it easier, I guess - you only need to find the distance from D to AC and compare it to the distance from B to AC.
Cut-the-Knot has a great applet here: Archimedes Triangle and Squaring of Parabola. This actually uses points external to the parabola, but it would suffice.
All the best with it.
4 May 2015 at 8:04 pm [Comment permalink]
Dear Murray
I am very interested in Math subject as it is my fovourat, as i am always looking to find differents solutions to a problem.
And i love to participate to sove math puzzles.
9 Nov 2016 at 1:57 am [Comment permalink]
Area of openright parabola and its latus rectum plz answer
9 Nov 2016 at 9:09 am [Comment permalink]
@Prasanna: The best place to ask your question is on the IntMath Forum, Here's the appropriate section: Plane Analytic Geometry.
11 Oct 2017 at 6:08 pm [Comment permalink]
Archimedes was a short black man, as earlier Arab sources described him. But, later European historians transformed him into white man.
10 Aug 2018 at 1:13 am [Comment permalink]
Wow!
Can someone write a program in QBasic to read in values of base and height, and use the formula to compute the length of the parabola segment.Values of base and height must be positive.
10 Aug 2018 at 5:52 am [Comment permalink]
@James: This would be a good question for the IntMath Forum. Here's the appropriate section: Applications of Integration.