3. The Circle
Before we jump into the various formulas for a circle. Let's quickly define what a circle really is and why it's important. The Math Open Reference defines a circle as;
"A line forming a closed loop, every point on which is a fixed distance from a center point."
However, if you were to search around you'd find varying research and definitions make it confusing to understand how to exactly define a circle. We break down the various definitions in our article on What is a Circle? We can simplify the above definition of a circle to;
A circle is, a set of points equal distrance (radius) from a fixed point (center point) on a plane.
Now that we have a set definition for a circle, let's quickly define the variables involved in the formulas of a circle.
Area of a Circle (variable: A) is the area within the circle.
Circumference (variable: C) is the perimeter of the circle.
Pi (variable: π) is the distance from the center of a circle to any point on the circumference.
Radius (variable: r) is the distance from the center point of a circle to any point on the circumference.
Diameter (variable: d) is the distance, passing through the center of the circle, from any one point on the circumference to another opposite point on the circumference, or put another way it's 2 times the radius of the circle.
With this foundational understanding, we can now walk through solving the various formulas of a circle.
a. Circle Formulas
Area of a Circle
The area of a circle formula can be expressed as follows:
A = π r2
Finding a circle's area is a helpful tool for measuring the space within the circumference of a circle. Let's break down the equation and define the variables. The area of a circle is represented as A . On the other side of the equation we have π (Pi) multiplied by r2 (radius) squared.
A common mnemonic for remembering this formula you have learned in school is: "Pie are squared". Repeat that a few times to ensure you can quickly recall it to calculate the area of a circle on your next test!
An example for how to solve for the radius (r) in the area of a circle formula can be found in our Basic Algebra - 5. Formulas and Literal Equations lesson.
Diameter of a Circle
The diameter of a circle formula can be expressed as follows:
D = 2 r
As mentioned above the diameter of a circle is simply two times the length of the radius of the circle. It's the longest distance between two points within the circumference of a circle.
Circumference of a Circle
The circumference of a circle formula can be expressed as follows:
C = 2πr
The circumference of a circle can be found by multiplying 2 times π multiplied by the radius r. The circumference is equally as important as the area of a circle equation in real life. Imagine a standing at the edge of a circular ice rink, you can skate from the edge to the center of the rink to find the radius, and continuing to the opposite edge you can find the diameter. Now, knowing Pi is a constant π = 3.14 you can now solve for all the circle formuals and find the skating rinks area, diameter, and circumference.
We can now advance to more complex circle formulas.
Center at the Origin
The circle with center (0, 0) and radius r has the equation:
x2 + y2 = r2
This means any point (x, y) on the circle will give the radius squared when substituted into the circle equation.
Center not at the Origin
The circle with centre (h, k) and radius r has the equation:
(x − h)2 + (y − k)2 = r2
These formulas are a direct result of Pythagoras' Formula for the length of the hypotenuse of a right triangle.
Need Graph Paper?
Example 1
Sketch the circle x2 + y2 = 4.
Find the center and radius first.
Answer
The equation is in the form x2 + y2 = r2, so we have a circle, center (0, 0) with radius `r=sqrt4=2`.
Example 2
Sketch the circle (x − 2)2 + (y − 3)2 = 16
Find the center and radius first.
Answer
The equation is in the form (x − h)2 + (y − k)2 = r2, so we have a circle with centre at (2, 3) and the radius is `r=sqrt(16)=4`.
Example 3
Sketch the circle (x + 4)2 + (y − 5)2 = 36
Answer
The equation is in the form (x − h)2 + (y − k)2 = r2.
We have a circle with centre at (−4, 5) and the radius is `r=sqrt(36)=6`.
Be careful with positive and negative x- and y-values in this work!
b. The General Form of the Circle
An equation which can be written in the following form (with constants D, E, F) represents a circle:
x2 + y2 + Dx + Ey + F = 0
This is called the general form of the circle.
Example 4
Find the centre and radius of the circle
x2 + y2 + 8x + 6y = 0
Sketch the circle.
Answer
Please revise Completing the Square first...
Our aim is to get the equation into the form: (x − h)2 + (y − k)2 = r2
We complete the square on the x-related portion and on the y-related portion, at the same time.
`x^2+y^2+8x+6y=0`
Group the x parts together and the y parts togther:
`(x^2+8x)+(y^2+6y)=0`
Complete the square on each of the x and y parts.
`(x^2+8x+16)+(y^2+6y+9)` `=16+9` `=25`
`(x+4)^2+(y+3)^2=5^2`
This is now in the format we require and we can determine the center and radius of the circle.
So the centre of the circle is (−4, −3) and the radius is 5 units.
Note that the circle passes through (0, 0). This is logical, since:
- The circle has radius 5
- Considering the right triangle formed by the points (−4, −3), (0, −3), and (0, 0), we can apply Pythagoras' Theorem and obtain: (−4)2 + (−3)2 = (5)2
- The formula for a circle follows from Pythagoras' Theorem.
Exercises
1. Find the equation of the circle with centre `(3/2, -2)` and radius `5/2`.
Answer
Centre `(3/2, -2)` radius `5/2`.
General form of the equation of a circle:
`(x-h)^2+(y-k)^2=r^2`
The required equation for this case:
`(x-3/2)^2+(y-(-2))^2=(5/2)^2`
`(x-3/2)^2+(y+2)^2=(5/2)^2`
There is no need to expand this out, since this is the most useful form of the equation.
2. Determine the centre and radius and then sketch the circle:
3x2 + 3y2 − 12x + 4 = 0
Answer
We complete the square as we did in an earlier example above.
First, we collect the x parts together and the y parts together, then divide throughout by 3.
`3x^2+3y^2-12x+4=0`
`3x^2-12x+3y^2+4=0`
`x^2-4x+y^2+4/3=0`
Then we complete the square on the x part. We do not need to do so for the y part because there is no single y term (only a y2 term).
`(x^2-4x+4)+y^2+4/3=4`
`(x-2)^2+y^2=4-4/3`
`(x-2)^2+y^2=8/3`
So the circle has centre `(2,0)` and has radius `sqrt(8/3)~~1.63`.
3. Find the points of intersection of the circle
x2 + y2 − x − 3y = 0
with the line
y = x − 1.
Answer
We solve the 2 equations simultaneously by substituting the expression
`y = x -1`
into the expression
`x^2+y^2-x-3y=0`
[See some background to this at: Algebraic Solution of Systems of Equations.]
We have:
`x^2+(x-1)^2-x-3(x-1)=0`
`x^2+x^2-2x+1-x-3x+3=0`
`2x^2-6x+4=0`
`x^2-3x+2=0`
`(x-1)(x-2)=0`
So we see that the solutions for x are `x = 1` or `x = 2`. This gives the corresponding y-values of `y = 0` and `y = 1`.
So the points of intersection are at: `(1, 0)` and `(2, 1)`.
We can see that our answer is correct in a sketch of the situation:
Exercise for You
Where did (0.5, 1.5) for the center of the circle come from?
Conic section: Circle
How can we obtain a circle from slicing a cone?
Each of the lines and curves in this chapter are conic sections, which means the curves are formed when we slice a cone at a certain angle.
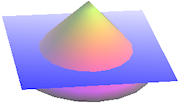
If we slice a cone with a plane at right angles to the axis of the cone, the shape formed is a circle.
