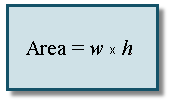5. Formulas and Literal Equations
It is very common in science and engineering to have a formula that needs re-arranging so that a variable that is originally on the right hand side becomes the subject of the formula, on the left.
In this section, we need to find an expression (involving letters and numbers) which is equal to a particular given letter. [Hence "literal" equation].
This is an important skill - you'll use it all the time in math and science (and engineering, too).
We simply solve the equation like we did in the previous
Solving Equations section, by balancing both sides.
Example 1
We recall the area of a rectangle with width w and height h.
A = w × h
Express the formula in terms of the height.
Answer
We need h on the left hand side by itself so our first step is to swap sides:
w × h = A
Dividing both sides by w gives:
`h=A/w`
Why do we want to do this? We may have hundreds of measurements of area and width for rectangles, and we need to find the height of each one. By manipulating the formula like this, we don't have to solve the equation every time.
Example 2
The area of a circle is given by
A = π r2
Solve for r.
Answer
We need r on the left hand side.
Swapping the sides:
π r2 = A
Dividing by π:
`r^2=A/pi`
Finding the (positive) square root of both sides:
`r=sqrt(A/pi)`
Note: There should be a ± in front of the square root, but we cannot have a negative radius, so we do not include the negative case.
See also √16 - How many answers?
Example 3
The formula for the area of a trapezoid is given by:
`A=h/2(x_1+x_2)`
where h is the height of the trapezoid and x1, x2 are the lengths of the parallel sides.
Solve the formula for x1.
Answer
`A=h/2(x_1+x_2)`
Multiply both sides by 2:
2A = h(x1 + x2)
Divide both sides by h:
`(2A)/h=x_1+x_2`
Finally, subtract x2 from both sides and then swap the sides so x1 is on the left:
`x_1=(2A)/h-x_2`
Now x1 is the subject of the formula.
Example 4
The pressure in an airtight container is given by the following formula. Solve for P1:
P = 0.05(P2 − P1)
Answer
`P = 0.05(P_2-P_1)`
To get P1 by itself, we first need to divide both sides by 0.05.
Recall that:
`0.05=5/100=1/20`
So our question means the same as:
`P = 1/20(P_2-P_1)`
So we multiply both sides by 20 (which means the same as dividing both sides by 0.05), to get:
`20P = P_2-P_1`
Add P1 to both sides:
`P_1+20P = P_2`
Subtract 20P from both sides:
`P_1 = P_2 - 20P`
Now P1 is the subject of the formula.