6. Applied Verbal Problems

Mathematics is really about solving problems, not just about moving letters and numbers around.

Most real-world problems are stated using words and we need to translate them into mathematical statements.

You need to:


For this section, you will need to know:

We will see how to solve each problem using two methods:

You can decide which method you understand best, but if you can follow the simultaneous equations method, it is probably best for future problems.

Good luck!

Example 1

water tank and pipes
Tank and pipes.
Source: Sustainable sanitation

Water is being drained out of a tank through 2 pipes at the rate of 330L/min. We know that one pipe releases 50L/min more than the other. How much do the 2 pipes drain each?


Solution A: Using one variable:

Solution B: Using 2 variables and simultaneous equations:

Example 2

beam
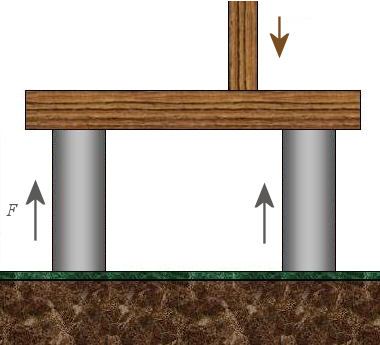
Builders constructing roof beams.

A beam is being supported by 2 pillars. The downwards force (due to gravity) must equal the sum of the 2 upwards forces due to the 2 pillars. Such a system is said to be in equilibrium. The second of the two forces is 6.4 N more than the first and the third is four times the first.

What are the 3 forces? (We are taking the positive magnitude of the forces only.)

Vocabulary

Sometimes a question will have some words which you may not know. In this question:

Pillar: A support column.

Equilibrium: Forces are in "equilibrium" if they cancel each other out.

Beam: A beam is normally made of timber, steel or concrete and holds up a roof (or similar).

Before answering this question, let's look at a query from a reader.

Reader's Question

Dale wrote:

How can the the third force and first force be three times the first force? I just don't get it. How can the first force be three times it self when it is equal to its self? It just confused me.

Solution A: Using one variable:

Solution B: Using 3 variables and simultaneous equations:

Example 3

vial containing drug
Vial of liquid.
Source: Helena Liu, Flickr

A vial contains 2 g of a drug which is required for two dosages. One of the patients is a small child and the other is a large adult who needs to get 660 mg more of the drug than the child. How much should be administered to each?

(Vocabulary: A vial is a container for storing liquid).


Solution A: Using one variable:

Solution B: Using 2 variables and simultaneous equations:

Example 4

scooter
Scooter
Source: RaeAllen

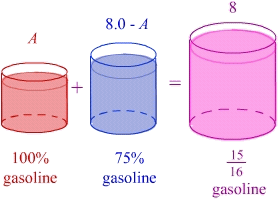
The manufacturer of a scooter engine recommends a gasoline-oil fuel mixture ratio of 15 to 1. In a particular garage, we can buy pure gasoline and a gasoline-oil mixture, which is 75% gasoline.

How much gasoline and how much of the gasoline-oil mix do we need to make 8.0 L of fuel for the scooter engine?


Solution A: Using one variable:

Solution B: Using 2 variables and simultaneous equations:

Didn't find what you are looking for on this page? Try search:

Online Algebra Solver

This algebra solver can solve a wide range of math problems. (Please be patient while it loads.)

Online algebra solver - can solve your math problems step-by-step

Algebra Lessons on DVD

get MathTutorDVDs

Easy to understand algebra lessons on DVD. See samples before you commit.

More info: Algebra videos

Ready for a break?

shadow factory

Play a math game.

(Well, not really a math game, but each game was made using math...)

The IntMath Newsletter

Sign up for the free IntMath Newsletter. Get math study tips, information, news and updates each fortnight. Join thousands of satisfied students, teachers and parents!

Given name: * required

Family name:

email: * required

See the Interactive Mathematics spam guarantee.

Share IntMath!

Short URL for this Page

Save typing! You can use this URL to reach this page:

intmath.com/verbal