IntMath forum | Introduction to Vectors
Vectors [Solved!]
asad 07 Oct 2016, 07:45
My question
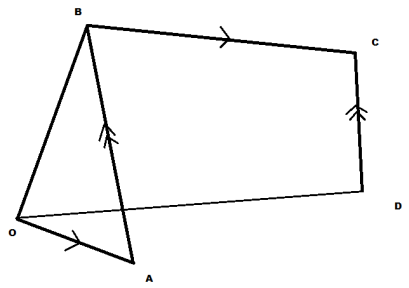
In the figure (also at http://prnt.sc/cqth0m), vector OB is three times longer than OA, BC is parallel to OA and twice its length. CD is parallel to BA.
Angle AOB = 60 degrees. If A and B have position vectors a and b respectively relative to O; and CD = kBA, find:
a) vector expression for BA and OD
b) find k if OD is perpendicular to AB
Relevant page
Vectors
What I've done so far
(a) BA = BO + OA = -b + a = a-b
Now how to find OD?
Since OB = 3OA, does this mean b=3a? And what is use of this information?
BC=2OA
CD=pBA
OD= OB+BC+CD = b+2a+p(a-b),which is not correct I know
For (b),AB would be =b-a, and OD would be found from (a), but what happens if it is perpendicular?
X
<img src="/forum/uploads/imf-3239-ques.png" width="409" height="288" alt="vectors" />
In the figure (also at <a href="http://prnt.sc/cqth0m">http://prnt.sc/cqth0m</a>), vector OB is three times longer than OA, BC is parallel to OA and twice its length. CD is parallel to BA.
Angle AOB = 60 degrees. If A and B have position vectors a and b respectively relative to O; and CD = kBA, find:
a) vector expression for BA and OD
b) find k if OD is perpendicular to AB
Relevant page
<a href="http://www.intmath.com/forum/vectors-39/vectors:108">Vectors</a>
What I've done so far
(a) BA = BO + OA = -b + a = a-b
Now how to find OD?
Since OB = 3OA, does this mean b=3a? And what is use of this information?
BC=2OA
CD=pBA
OD= OB+BC+CD = b+2a+p(a-b),which is not correct I know
For (b),AB would be =b-a, and OD would be found from (a), but what happens if it is perpendicular?
Re: Vectors
Murray 08 Oct 2016, 23:37
Hi Asad
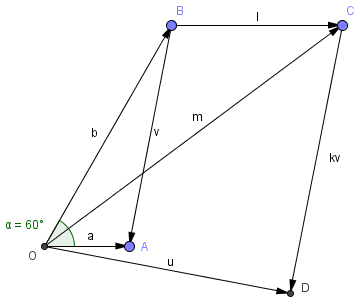
As some general hints for this kind of question, it's good to separate the vector diagram (where you use vector addition and subtraction, as you've done in the first part of your answer), and the related scalar diagram, where you just deal with the lengths involved.
(Just a small point - your question has `k` as the unknown variable, and then you have used `p` in your answer. Let's stick to `k`.)
It's not so easy to see what's going on in the given diagram (that's probably deliberate on the part of the question writers).
Here's the vector diagram, this time drawn to scale (I've used GeoGebra to draw the diagram):
You wrote:
(a) BA = BO + OA = -b + a = a-b
Yes, OK.
Now how to find OD?
Since OB = 3 OA, does this mean b = 3a?
Actually, no. This is what I meant about separating out the vector and scalar diagrams. Vector b is 3 times longer than vector a, but they are pointing in different directions, so we can't say b = 3a.
And what is use of this information?
We'll use it in the scalar diagram.
BC = 2OA
CD = `k`BA
OD = OB + BC + CD = b + 2a + `k`(a-b), which is not correct I know
Actually, I think it is correct (with the `p` changed back to `k`)!
For (b), AB? would be =b-a, and OD would be found from (a), but what happens if it is perpendicular?
Before going on to this, can you draw a scalar diagram now, showing the known lengths? It will help a lot, I think.
X
Hi Asad
As some general hints for this kind of question, it's good to separate the <b>vector</b> diagram (where you use vector addition and subtraction, as you've done in the first part of your answer), and the related <b>scalar</b> diagram, where you just deal with the lengths involved.
(Just a small point - your question has `k` as the unknown variable, and then you have used `p` in your answer. Let's stick to `k`.)
It's not so easy to see what's going on in the given diagram (that's probably deliberate on the part of the question writers).
Here's the vector diagram, this time drawn to scale (I've used GeoGebra to draw the diagram):
<img src="/forum/uploads/imf-2519-vector-diagram.png" width="360" height="307" alt="Vectors" />
You wrote:
<blockquote>(a) <b>BA = BO + OA = -b + a = a-b</b></blockquote>
Yes, OK.
<blockquote>Now how to find <b>OD</b>?
Since <b>OB</b> = 3 <b>OA</b>, does this mean <b>b = 3a</b>?</blockquote>
Actually, no. This is what I meant about separating out the vector and scalar diagrams. Vector <b>b</b> is 3 times longer than vector <b>a</b>, but they are pointing in different directions, so we can't say <b>b = 3a</b>.
<blockquote>And what is use of this information?</blockquote>
We'll use it in the scalar diagram.
<blockquote><b>BC</b> = 2<b>OA</b>
<b>CD</b> = `k`<b>BA</b>
<b>OD = OB + BC + CD = b + </b>2<b>a</b> + `k`<b>(a-b)</b>, which is not correct I know</blockquote>
Actually, I think it is correct (with the `p` changed back to `k`)!
<blockquote>For (b), <b>AB</b>? would be <b>=b-a</b>, and <b>OD</b> would be found from (a), but what happens if it is perpendicular?</blockquote>
Before going on to this, can you draw a scalar diagram now, showing the known lengths? It will help a lot, I think.
Re: Vectors
Murray 26 Oct 2016, 23:39
It seems Asad has disappeared. Anyone else like to have a go at finishing it?
X
It seems Asad has disappeared. Anyone else like to have a go at finishing it?
Re: Vectors
stephenB 29 Nov 2016, 21:11
OK, I'll have a go.
I used GeoGebra (great tool for these problems) for a scalar diagram, as Murray suggested.
There may be an easier way, but this is how I did it.
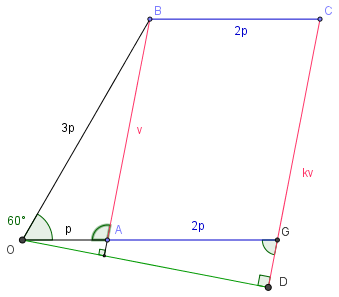
I've put all the known values on the graph. I extended OA to intersect CD at G.
We can find length AB using cosine rule:
`c^2 = a^2 + b^2 - 2ac cosC`
`v^2 = (3p)^2 + p^2 - 2(3p)(p)cos60^"o"`
`v^2 = 9p^2 + p^2 - 6p^2(0.5)`
`v^2 = 7p^2`
`v = p sqrt(7)`
Using that, we can find the angle OAB and the sine rule
`a/(sin A) = c/(sin c)`
`(3p)/(sin A) = (psqrt7)/(sin 60^"o")`
Cancelling the `p`'s and turning it all upside down:
`(sin A)/3 = (sin 60^"o")/sqrt(7)`
`sin A = 0.98198050606`
`A` is more than 90 deg, so
`A = 180 - 79.1066054 = 100.8933946^"o"`
Since AB and CD are parallel, by alternate angles we can say angle OGD is 79.1066054^"o".
Using that, we can find length GD using the fact OGD is a right triangle.
`cos 79.1066054^"o" = (GD)/(3p)`
So `GD = 3p (0.18898223566) = 0.56694670698p`
So CD = CG + GD = `p sqrt(7)+0.56694670698p = 3.21269801805p`
Since AB = `p sqrt(7)`,
`k = (3.21269801805p)/(psqrt(7)) = 1.21428571333`
According to the measuring tool in GeoGebra, this is a correct answer.
Does it look right?
Yours
Stephen
X
OK, I'll have a go.
I used GeoGebra (great tool for these problems) for a scalar diagram, as Murray suggested.
There may be an easier way, but this is how I did it.
<img src="/forum/uploads/imf-4812-vector-diagram-scalar.png" width="339" height="297" alt="Vectors" />
I've put all the known values on the graph. I extended OA to intersect CD at G.
We can find length AB using cosine rule:
`c^2 = a^2 + b^2 - 2ac cosC`
`v^2 = (3p)^2 + p^2 - 2(3p)(p)cos60^"o"`
`v^2 = 9p^2 + p^2 - 6p^2(0.5)`
`v^2 = 7p^2`
`v = p sqrt(7)`
Using that, we can find the angle OAB and the sine rule
`a/(sin A) = c/(sin c)`
`(3p)/(sin A) = (psqrt7)/(sin 60^"o")`
Cancelling the `p`'s and turning it all upside down:
`(sin A)/3 = (sin 60^"o")/sqrt(7)`
`sin A = 0.98198050606`
`A` is more than 90 deg, so
`A = 180 - 79.1066054 = 100.8933946^"o"`
Since AB and CD are parallel, by alternate angles we can say angle OGD is 79.1066054^"o".
Using that, we can find length GD using the fact OGD is a right triangle.
`cos 79.1066054^"o" = (GD)/(3p)`
So `GD = 3p (0.18898223566) = 0.56694670698p`
So CD = CG + GD = `p sqrt(7)+0.56694670698p = 3.21269801805p`
Since AB = `p sqrt(7)`,
`k = (3.21269801805p)/(psqrt(7)) = 1.21428571333`
According to the measuring tool in GeoGebra, this is a correct answer.
Does it look right?
Yours
Stephen
Re: Vectors
Murray 30 Nov 2016, 01:08
Stephen
This looks good to me!
Thanks for your solution.
Regards
Murray
X
Stephen
This looks good to me!
Thanks for your solution.
Regards
Murray
Re: Vectors
joedenly 05 Apr 2019, 02:40
Thannks for sharing the information with us.
X
Thannks for sharing the information with us.
Re: Vectors
JK123 12 Aug 2021, 01:31
helpful post, thanks for sharing the solution
X
helpful post, thanks for sharing the <a href="https://en.wikipedia.org/wiki/Main_Page">solution</a>
Related Vectors questions
- differentiating xihat+yjhat+zkhat. [Solved!]
How is it done in a simpler example.
(x^2+y^2+z^2) times [xihat+yjhat+zkhat divided by sqrt (x^2+y^2+z^2)] 6761hash 11 Aug 2017, 08:27
- Vectors [Solved!]
In the diagram
AB = p
CA = q
... Swalay 05 Sep 2016, 06:25
- Vector from angle [Solved!]
I have the angles representing the suns position on the sky.
170 degrees south
35 degrees elevation
Now,... Balder 05 Apr 2016, 04:05
- Vectors question [Solved!]
Let U,V & W be 3 vectors,which of the following make sense and which... James 18 Dec 2015, 10:39
Vectors lessons on IntMath
top


