Swalay 05 Sep 2016, 06:25
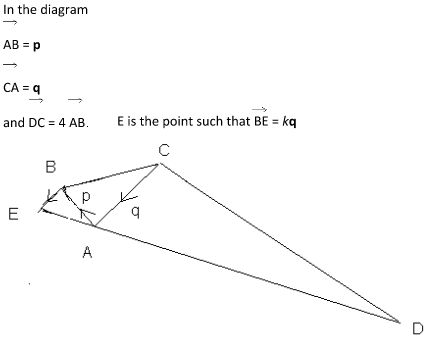
In the diagram
AB = p
CA = q
and DC = 4 AB
E is the point such that BE = kq
d) Given that D, A and E lie on a straight line find the value of k.????
Answers so far:
a) DC+CA=DA
Hence DA = 4p + q
b) Again CB = CA+AB
Hence CB = q + p
c) Again AE = AB + BE
Therefore AE= p + kq
X
<img src="/forum/uploads/imf-triangle.jpg" width="427" height="340" alt="vectors" />
In the diagram
AB = p
CA = q
and DC = 4 AB
E is the point such that BE = kq
d) Given that D, A and E lie on a straight line find the value of k.????Relevant page
<a href="/vectors/3-vectors-2-dimensions.php">3. Vectors in 2 Dimensions</a>
What I've done so far
Answers so far:
a) DC+CA=DA
Hence DA = 4p + q
b) Again CB = CA+AB
Hence CB = q + p
c) Again AE = AB + BE
Therefore AE= p + kqMurray 05 Sep 2016, 22:18
@Swalay: What can you tell me about the lines AB and DC?
How about the lines CA and BE?
What can we conclude about the 2 triangles ?DCA and ?ABE?
X
@Swalay: What can you tell me about the lines AB and DC? How about the lines CA and BE? What can we conclude about the 2 triangles ?DCA and ?ABE?
Swalay 06 Sep 2016, 04:49
AB and DC are parallel
CA and BE are parallel
Triangles DCA and ABE are congruents
Thank you for your help so far
AB/BE=DA/CA
(P+kq)/kq = (4p+q)/q
k=1/4
X
AB and DC are parallel CA and BE are parallel Triangles DCA and ABE are congruents Thank you for your help so far AB/BE=DA/CA (P+kq)/kq = (4p+q)/q k=1/4
Murray 06 Sep 2016, 04:54
Actually, the triangles aren't congruent (which means same size, same shape), but similar (same shape, different size).
Your final answer is correct!
X
Actually, the triangles aren't <b>congruent</b> (which means same size, same shape), but <b>similar</b> (same shape, different size). Your final answer is correct!
You need to be logged in to reply.