1. Vector Concepts

Magnitude and Direction of a Vector

A vector is a quantity that has both magnitude and direction. (Magnitude just means 'size'.)

Examples of Vector Quantities:

• I travel 30 km in a Northerly direction (magnitude is 30 km, direction is North - this is a displacement vector)
• The train is going 80 km/h towards Sydney (magnitude is 80 km/h, direction is 'towards Sydney' - it is a velocity vector)
• The force on the bridge is 50 N acting downwards (the magnitude is 50 Newtons and the direction is down - it is a force vector)

Other examples of vectors include:

Acceleration, momentum, angular momentum, magnetic and electric fields

Each of the examples above involves magnitude and direction.

Note: A vector is not the same as a scalar. Scalars have magnitude only. For example, a speed of 35 km/h is a scalar quantity, since no direction is given. Other examples of scalar quantities are:

Volume, density, temperature, mass, speed, time, length, distance, work and energy.

Each of these quantities has magnitude only, and do not involve direction.

Vector Notation

We will use a bold capital letter to name vectors. For example, a force vector could be written as F.

Alternative vector notations

• Some textbooks write vectors using an arrow above the vector name, like this:
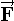
• You will also see vectors written using matrix-like notation. For example, the vector acting from (0, 0) in the direction of the point (2, 3) can be written

`[(2),(3)]`

A vector is drawn using an arrow. The length of the arrow indicates the magnitude of the vector. The direction of the vector is represented by (not surprisingly :-) the direction of the arrow.

Example 1 - Vectors

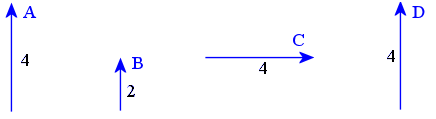
The displacement vector A has direction 'up' and a magnitude of 4 cm.

Vector B has the same direction as A, and has half the magnitude (2 cm).

Vector C has the same magnitude as A (4 units), but it has different direction.

Vector D is equivalent to vector A. It has the same magnitude and the same direction. It doesn't matter that A is in a different position to D - they are still considered to be equivalent vectors because they have the same magnitude and same direction. We can write:

A = D

Note: We cannot write A = C because even though A and C have the same magnitude (4 cm), they have different direction. They are not equivalent.

Free and Localized Vectors

So far we have seen examples of "free" vectors. We draw them without any fixed position.

Another way of representing vectors is to use directed line segments. This means the vector is named using an initial point and a terminal point. Such a vector is called a "localized vector".

Example 2 - Localized Vectors

A vector OP has initial point O and terminal point P. When using directed line segments, we still use an arrow for the drawing, with P at the arrow end. The length of the line OP is an indication of the magnitude of the vector.

We could have another vector RS as follows. It has initial point R and terminal point S.

Because the 2 vectors have the same magnitude and the same direction (they are both horizontal and pointing to the right), then we say they are equal. We would write:

OP = RS

Note that we can move vectors around in space and as long as they have the same vector magnitude and the same direction, then they are considered equal vectors.

Magnitude of a Vector

We indicate the magnitude of a vector using vertical lines on either side of the vector name.

The magnitude of vector PQ is written |PQ|.

We also used vertical lines like this earlier in the Numbers chapter (where it was called 'absolute value', a similar concept to magnitude).

So for example, vector A above has magnitude 4 units. We would write the magnitude of vector A as:

| A | `= 4`

Scalar Quantities

A scalar quantity is described by a numerical quantity and possibly a unit, but not direction.

For example, a pen may have length "10 cm". The length 10 cm is a scalar quantity - it has a size (10) and a unit (cm), but no direction is involved.

Examples of scalars include: area, volume, speed, mass, temperature, work, and power. A scalar can be positive or negative (and even complex).

Scalar Multiplication

We can increase or decrease the magnitude of a vector by multiplying the vector by a scalar.

Example 3 - Scalar Multiplication

In the examples we saw earlier, vector B (2 units) is half the size of vector A (which is 4 units) . We can write:

B = 0.5 A

This is an example of a scalar multiple. We have multiplied the vector A by the scalar 0.5.

Example 4 - Scalar Multiplication

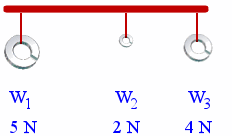
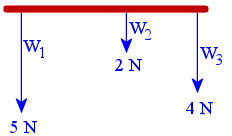
We have 3 weights tied to a beam.

The first weight is W₁ = 5 N, the second is W₂ = 2 N and the third is W₃ = 4 N.

We can represent these weights using a vector diagram (where the length of the vector represents the magnitude) as follows:

They are vectors because they all have a direction (down) and a magnitude.

Each of the following scalar multiples is true for this situation:

Since `5 = 2.5 × 2`, we can write:

W₁ = 2.5 W₂

Since `2 = 0.5 × 4`, we can write:

W₂ = 0.5 W₃

Since `4 = 0.8 × 5`, we can write:

W₃ = 0.8 W₁

Each of these statements is a scalar multiplication.

Vectors in Opposite Directions

We have 2 teams playing a tug-of-war match. At the beginning of the game, they are very evenly matched and are pulling with equal force in opposite directions. We could name the vectors OA and OB.

We can represent the tug of war using a vector diagram:

We note that the magnitude of each vector is the same, but they are acting in opposite directions. In such a case, we indicate the opposite directions by use of a negative sign.

So we write:

OA = −OB

Zero Vectors

A zero vector has magnitude of 0. It can have any direction.

A vector may have zero magnitude at an instance in time. For example, a boat bobbing up and down in the water will have a positive velocity vector when moving up, and a negative velocity vector when moving down. At the instant when it is at the top of its motion, the magnitude is zero.

In the tug-of-war example above, the teams are evenly matched at a certain instant and neither side is able to move. In this case, we would have:

OA + OB = 0

The 2 force vectors OA and OB, operating in opposite directions, cancel each other out.

Unit Vectors

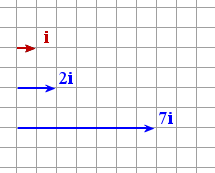
A unit vector has length 1 unit and can take any direction.

A one-dimensional unit vector is usually written i.

Example 5 - Unit Vector

In the following diagram, we see the unit vector (in red, labeled i) and two other vectors that have been obtained from i using scalar multiplication (2i and 7i).