9. Vectors with Variable Magnitude and Direction
Vectors can change magnitude and direction over time. For example, the forces on the components in an engine change direction and magnitude thousands of times a minute.
For a 2-dimensional vector, the x- and y-components of the vector will be functions of t. In general, we would write:
P = x(t) i + y(t) j
Example 1: 2-dimensional Variable Vector
A vector F represents a variable force (in newtons) at time t (in seconds) is given by
F = (3t2 + 5) i + (4t) j
At t = 0 s, this vector will have value
F
= (5 i + 0 j) N
= 5 i N
At t = 5 s, the vector has value
F = (80 i + 20 j) N
What have we just done?
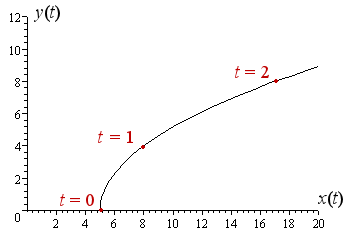
The following graph represents the position of the terminal point of our variable vector at time `t`. The first 2 seconds are shown and each whole second is marked with a red dot.
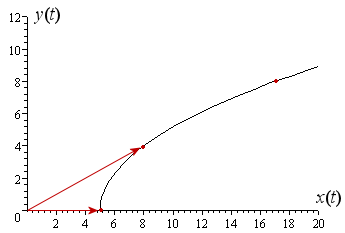
At time t = 0 s, the vector has value `5` i which means it is only acting in the x-direction at that time. There is no y-component.
At time t = 1 s, the terminal point is at `(8, 4)` and we write the value of the vector at that time as (8 i + 4 j) N.
The vectors at the particular times t = 0 s and t = 1 s are shown on the following graph as red arrows:
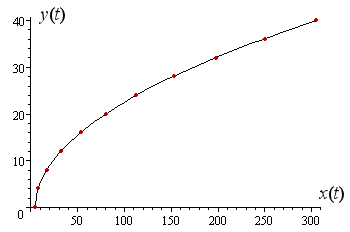
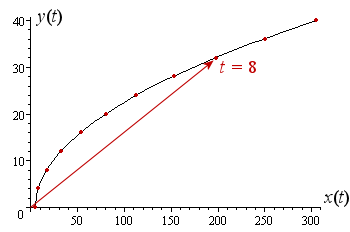
Now we zoom out and have a look at a longer time scale (the first `10` seconds).
The value of the vector at time t = 8 s is F = 197 i + 32 j N and this is shown below:
The shape of the curve is parabolic. The vector's magnitude increases as time increases and the angle changes as well (it initially increases to about `t = 2` and then decreases.)
3-dimensional Variable Vectors
For 3-dimensional vectors, we extend the above 2-dimensional case. Our variable three-dimensional vector has the general form:
P = x(t) i + y(t) j + z(t) k
Example 2: 3-dimensional variable vector
A is an acceleration vector that varies with time, given by:
A = (5t) i + (2t + 3) j + (t2 + 10) k
The units are m/s2.
At `t = 0`, the vector has value:
A
= (0) i + (3) j + (10) k
= 3 j + 10 k m/s2
At `t = 4`, the vector has value:
A = 20 i + 11 j + 26 k m/s2
What have we done?
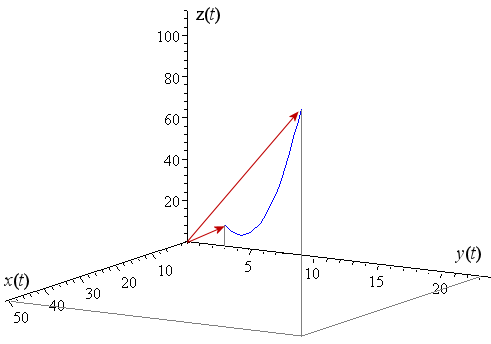
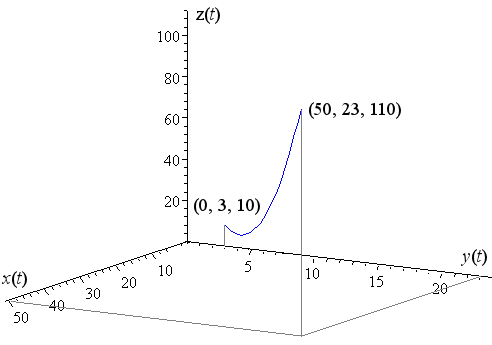
Here is the first 10 seconds of our 3-dimensional curve. It starts at the point (0, 3, 10) and finishes at (50, 23, 110).
The curve is parabolic and it is coming towards us, out of the "page".
The following graph shows the position of the vector at `t = 0\ "s"` (the lower one) and also at `t = 10\ "s"` (the upper one).