6. The 3-dimensional Co-ordinate System

We can expand our 2-dimensional (x-y) coordinate system into a 3-dimensional coordinate system, using x-, y-, and z-axes.

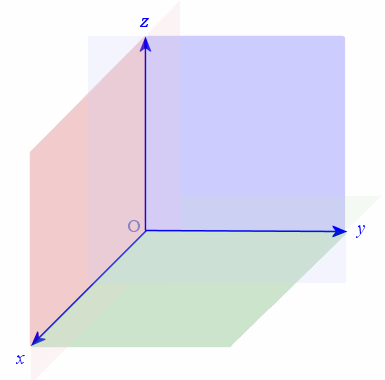
The x-y plane is horizontal in our diagram above and shaded green. It can also be described using the equation z = 0, since all points on that plane will have 0 for their z-value.

The x-z plane is vertical and shaded pink above. This plane can be described using the equation `y = 0`.

The y-z plane is also vertical and shaded blue. The y-z plane can be described using the equation `x = 0`.

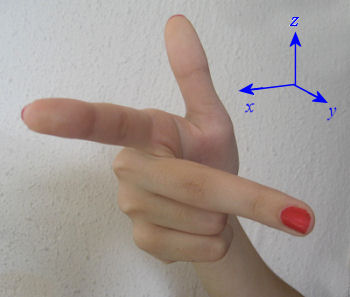
We normally use the 'right-hand orientation' for the 3 axes, with the positive x-axis pointing in the direction of the first finger of our right hand, the positive y-axis pointing in the direction of our second finger and the positive z-axis pointing up in the direction of our thumb.

Example - Points in 3-D Space

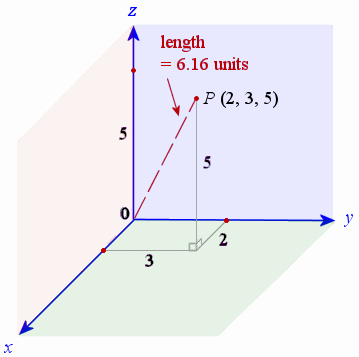
In 3-dimensional space, the point `(2, 3, 5)` is graphed as follows:

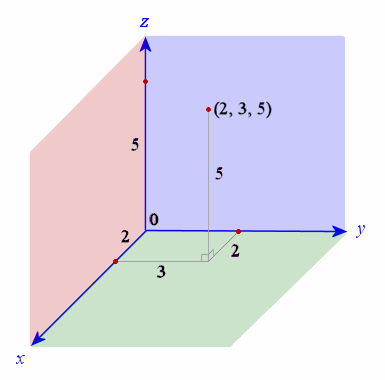
To reach the point `(2, 3, 5)`, we move `2` units along the x-axis, then `3` units in the y-direction, and then up `5` units in the z-direction.

You can explore this example in 3D space using this applet:

3D Space Interactive Applet

Distance in 3-dimensional Space

To find the distance from one point to another in 3-dimensional space, we just extend Pythagoras' Theorem.

Distance from the Origin

The general point P (a, b, c) is shown on the 3D graph below. The point N is directly below P on the x-y plane.

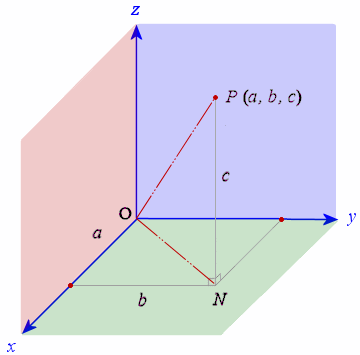
The distance from `(0, 0, 0)` to the point P (a, b, c) is given by:

`"distance"\ OP = sqrt (a^2+ b^2+ c^2)`

Why?

The point N `(a, b, 0)` is shown on the graph. From Pythagoras' Theorem,

`"distance"\ ON = sqrt (a^2+ b^2)`

and squaring both sides gives:

`(ON)^2=a^2+b^2`

Distance NP is simply c (this is the distance up the z-axis for the point P).

Applying Pythagoras' Theorem for the triangle ONP, we have:

`"distance"\ OP = sqrt ((ON)^2+ c^2)`

`= sqrt (a^2+ b^2+ c^2)`

Example 1 - Distance from the Origin to a Point

Find the distance from the origin O to the point B `(2, 3, 5)`. This is the example from above.

Answer

Distance Between 2 Points in 3 Dimensions

If we have point A (x₁, y₁, z₁) and another point B (x₂, y₂, z₂) then the distance AB between them is given by the formula:

`"distance"\ AB = ` `sqrt ((x_2-x_1)^2+ (y_2-y_1)^2+ (z_2-z_1)^2)`

This is just an extension of the distance formula (from the origin to a point) that we met above.

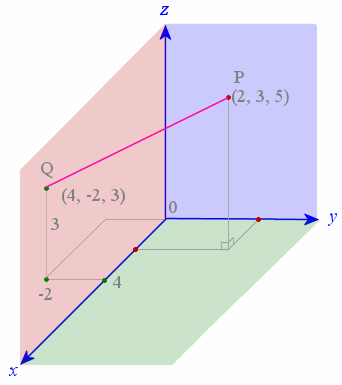
Example 2 - Distance between 2 points

Find the distance between the points P (2, 3, 5) and Q (4, -2, 3).

Answer