IntMath forum | Introduction to Vectors
Vector from angle [Solved!]
Balder 05 Apr 2016, 04:05
My question
I have the angles representing the suns position on the sky.
170 degrees south
35 degrees elevation
Now, I want to retrieve the vector components for the suns angle.
Please spread some light, I am stuck.
Thank you for any help.
Relevant page
Calculate 3d vector from angles with respect to x and y axis | Physics Forums - The Fusion of Science and Community
What I've done so far
I have tried Tan(Azimute), Tan(Elevation), 1
X
I have the angles representing the suns position on the sky.
170 degrees south
35 degrees elevation
Now, I want to retrieve the vector components for the suns angle.
Please spread some light, I am stuck.
Thank you for any help.
Relevant page
<a href="https://www.physicsforums.com/threads/calculate-3d-vector-from-angles-with-respect-to-x-and-y-axis.258525/">Calculate 3d vector from angles with respect to x and y axis | Physics Forums - The Fusion of Science and Community</a>
What I've done so far
I have tried Tan(Azimute), Tan(Elevation), 1
Re: Vector from angle
Murray 07 Apr 2016, 07:46
Balder
Yes, 3D geometry has a habit of giving your grey matter a good workout.
The link you pointed to is very similar to the problem you're asking about.
I'll try to help you see what's going on in that problem, and hopefully that will help you get started on yours.
The statement "60^"o" to the x-axis could simply mean this:
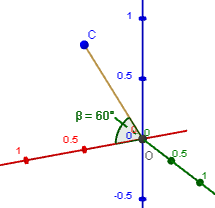
We have a unit vector pointing vertically upwards from the x-axis (which is the red axis pointing out to the left and down slightly. The y-axis is to the right, and z-axis is up in this particular system).
But really, there are (infinitely) many vectors at 60^"o" to that axis, all of them along a circle, like this:
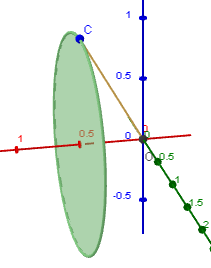
Now the other vector, the one that is 60^"o" to the y-axis, could be anywhere on the red circle shown:
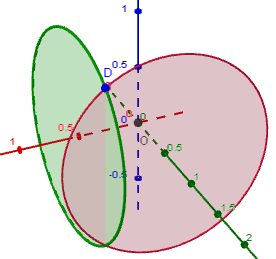
The vector from the origin to the intersection point of those 2 circles is where we are 60^"o" to both the x- and y-axes.
Getting a closer look at that intersection point (D), we have:
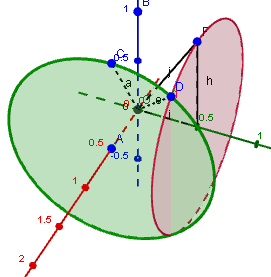
Finally, we see the vector OD by itself, and see the 45^"o" angle between it and the z-axis, as they found in that problem.
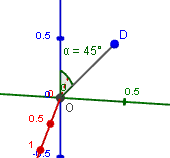
(There will be a second vector for the second intersection point, but it is also at 45^"o" to the z-axis.)
Now to your problem. You will also have 2 circles which will intersect, and from there will need to work out the resulting vectors.
Do you think your can get started?
As a suggestion, I'd make the x-axis to be the North-South axis, the y-axis to be your East-West axis, and the z-axis as the vertical axis.
Let us know how far you get and we'll help if you're stuck again.
Regards
Murray
BTW, I made these images using Geogebra. It's a great (free) tool for drawing things in 3D (and 2D).
X
Balder
Yes, 3D geometry has a habit of giving your grey matter a good workout.
The link you pointed to is very similar to the problem you're asking about.
I'll try to help you see what's going on in that problem, and hopefully that will help you get started on yours.
The statement "60^"o" to the <i>x</i>-axis could simply mean this:
<img src="/forum/uploads/imf-3254-vectors-1.png" width="215" height="208" alt="vectors" />
We have a unit vector pointing vertically upwards from the <i>x</i>-axis (which is the red axis pointing out to the left and down slightly. The <i>y</i>-axis is to the right, and <i>z</i>-axis is up in this particular system).
But really, there are (infinitely) many vectors at 60^"o" to that axis, all of them along a circle, like this:
<img src="/forum/uploads/imf-3507-vectors-2.png" width="211" height="268" alt="vectors" />
Now the other vector, the one that is 60^"o" to the <i>y</i>-axis, could be anywhere on the red circle shown:
<img src="/forum/uploads/imf-3805-vectors-3.png" width="276" height="259" alt="vectors" />
The vector from the origin to the intersection point of those 2 circles is where we are 60^"o" to both the <i>x</i>- and <i>y</i>-axes.
Getting a closer look at that intersection point (D), we have:
<img src="/forum/uploads/imf-4018-vectors-8.png" width="271" height="277" alt="vectors" />
Finally, we see the vector OD by itself, and see the 45^"o" angle between it and the <i>z</i>-axis, as they found in that problem.
<img src="/forum/uploads/imf-4157-vectors-9.png" width="170" height="158" alt="vectors" />
(There will be a second vector for the second intersection point, but it is also at 45^"o" to the <i>z</i>-axis.)
Now to your problem. You will also have 2 circles which will intersect, and from there will need to work out the resulting vectors.
Do you think your can get started?
As a suggestion, I'd make the <i>x</i>-axis to be the North-South axis, the <i>y</i>-axis to be your East-West axis, and the <i>z</i>-axis as the vertical axis.
Let us know how far you get and we'll help if you're stuck again.
Regards
Murray
BTW, I made these images using Geogebra. It's a great (free) tool for drawing things in 3D (and 2D).
Re: Vector from angle
Balder 07 Apr 2016, 10:26
Dear Murray, I don't see the two circles intersect with 170 degrees south and 35 degrees elevation. What am I missing?
I am really stuck, so a little more help is greatly appreciated.
Thanks!
X
Dear Murray, I don't see the two circles intersect with 170 degrees south and 35 degrees elevation. What am I missing?
I am really stuck, so a little more help is greatly appreciated.
Thanks!
Re: Vector from angle
Murray 07 Apr 2016, 23:41
Balder
Sorry, but in my enthusiasm to include the images for the Physics Forum example, I didn't think enough about your example.
In fact, in your case, the two vectors are fixed, not an infinite bunch of vectors around a circle.
I'll give you some images of your situation, and some hints.
As I suggested before, I'm using the positive x-axis for north (the red one heading to the top left of the image), the (negative) y-axis is East (the green axis going approximately left-right in the image), and the positive z-axis is up.
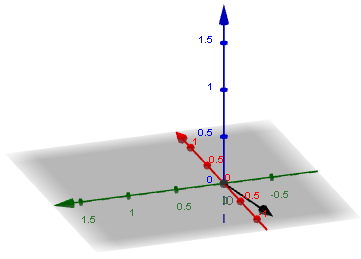
The image shows the 170^"o" vector (170^"o" clockwise from North, which means it's almost due South). This vector is on the x-y plane, which is shaded grey.
It's a unit vector. Can you figure out its coordinates?
Hint: You could start on any point on the negative x-axis, say (-5,0,0). Let's call it point P. From there you need to go 5 tan 10^"o" in the Easterly direction. That give you point Q.
To get the unit vector, you just divide the vector OQ you just found by the length of the vector OQ.
Let's just complete that part to make sure it makes sense before going on to the elevation part.
Regards
Murray
X
Balder
Sorry, but in my enthusiasm to include the images for the Physics Forum example, I didn't think enough about your example.
In fact, in your case, the two vectors are fixed, not an infinite bunch of vectors around a circle.
I'll give you some images of your situation, and some hints.
As I suggested before, I'm using the positive <i>x-</i>axis for north (the red one heading to the top left of the image), the (negative) <i>y-</i>axis is East (the green axis going approximately left-right in the image), and the positive <i>z-</i>axis is up.
<img src="/forum/uploads/imf-2056-vectors-x1.png" width="361" height="259" alt="vectors" />
The image shows the 170^"o" vector (170^"o" clockwise from North, which means it's almost due South). This vector is on the <i>x-y</i> plane, which is shaded grey.
It's a unit vector. Can you figure out its coordinates?
Hint: You could start on any point on the negative <i>x-</i>axis, say (-5,0,0). Let's call it point P. From there you need to go <span class="intmath">5 tan 10^"o"</span> in the Easterly direction. That give you point Q.
To get the unit vector, you just divide the vector OQ you just found by the length of the vector OQ.
Let's just complete that part to make sure it makes sense before going on to the elevation part.
Regards
Murray
Re: Vector from angle
Balder 08 Apr 2016, 02:33
Dear Murray, I think what you explained is the same as Tan to the angle, isn't it?
X
Dear Murray, I think what you explained is the same as Tan to the angle, isn't it?
Re: Vector from angle
Murray 08 Apr 2016, 03:16
Balder
Yes, my hint (3rd paragraph), says "go 5 tan 10^"o" in the Easterly direction".
That will give you the y-value of the point Q.
It comes from
`tan theta = "opposite"/"adjacent"`.
In this case, we have
`tan 10^"o" = (PQ)/5`
So
`PQ = 5 tan 10^"o"`.
X
Balder
Yes, my hint (3rd paragraph), says "go <span class="intmath">5 tan 10^"o"</span> in the Easterly direction".
That will give you the <i>y</i>-value of the point Q.
It comes from
`tan theta = "opposite"/"adjacent"`.
In this case, we have
`tan 10^"o" = (PQ)/5`
So
`PQ = 5 tan 10^"o"`.
Re: Vector from angle
Balder 08 Apr 2016, 03:29
Hi Murray, what I want to accomplish is to get the components of a vector from 170 degrees south and 35 degrees elevation as simple as possible.
Initially I thought that Tan 170, Tan 35 an 1 would do the trick, but obviously not.
Then I tried to read several posts on the net implicating Cos to the various angles, but this has not worked out either.
May be, you could hint me directly to the answer and then I will try to figure why?
X
Hi Murray, what I want to accomplish is to get the components of a vector from 170 degrees south and 35 degrees elevation as simple as possible.
Initially I thought that Tan 170, Tan 35 an 1 would do the trick, but obviously not.
Then I tried to read several posts on the net implicating Cos to the various angles, but this has not worked out either.
May be, you could hint me directly to the answer and then I will try to figure why?
Re: Vector from angle
Murray 08 Apr 2016, 07:01
Hi Balder
I'm doing exactly that - in stages.
Could you figure out the point Q? I've basically already given it to you.
Regards
X
Hi Balder
I'm doing exactly that - in stages.
Could you figure out the point Q? I've basically already given it to you.
Regards
Re: Vector from angle
Balder 08 Apr 2016, 09:00
Yes, I've figured point Q.
X
Yes, I've figured point Q.
Re: Vector from angle
Murray 08 Apr 2016, 21:23
Assuming your answer for Q is (5, 0.8816, 0), the next step is to find the length of that vector (the distance OQ), then divide each of the values in (5, 0.8816, 0) by that length.
That will give us the unit vector.
It's best if you show your answer, then I know you're on the right track.
X
Assuming your answer for Q is (5, 0.8816, 0), the next step is to find the length of that vector (the distance OQ), then divide each of the values in (5, 0.8816, 0) by that length.
That will give us the unit vector.
It's best if you show your answer, then I know you're on the right track.
Re: Vector from angle
Balder 09 Apr 2016, 06:17
`OQ = ` `sqrt(5^2 + 0,8816^2) = 5.07712`
Unit vector equals `(5/5.07712, 0.8816/5.07712, 0/5.07712)` - right?
X
`OQ = ` `sqrt(5^2 + 0,8816^2) = 5.07712`
Unit vector equals `(5/5.07712, 0.8816/5.07712, 0/5.07712)` - right?
Re: Vector from angle
Murray 09 Apr 2016, 09:07
Yes, you are on the right track. The point Q can be simplified to:
`(0.9848, 0.1736, 0)`
Next step is to find the point R above Q, such that QOR is 35^"o".
Good luck!
BTW, I edited your math input answer, (so it looked like math) as follows:
(1) The surrounding symbol needs to be the backtick, not an apostrophe;
(2) The decimal symbol needs to be the period (.), not comma.
X
Yes, you are on the right track. The point Q can be simplified to:
`(0.9848, 0.1736, 0)`
Next step is to find the point R above Q, such that QOR is 35^"o".
Good luck!
BTW, I edited your math input answer, (so it looked like math) as follows:
(1) The surrounding symbol needs to be the backtick, not an apostrophe;
(2) The decimal symbol needs to be the period (.), not comma.
Re: Vector from angle
Balder 15 Apr 2016, 01:55
This is where I struggle.
May you show me what to do next?
X
This is where I struggle.
May you show me what to do next?
Re: Vector from angle
Murray 15 Apr 2016, 21:02
Here's what it looks like. We have the point R above point Q, forming a 35^"o" angle QOR. Length OQ is 1, because we made it so.
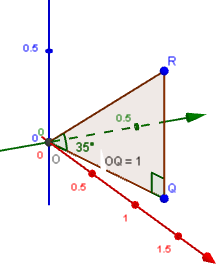
OQR is a right triangle, and we are trying to find the height RQ - let's call it h.
So we will use
`tan 35^"o" = h/1`
Once you have that, you have your vector components in each of the x-, y- and z-directions, which was your original question.
If needed, your could normalize the vector OR, using the same thing we did before (divide each component by the length of OR).
X
Here's what it looks like. We have the point R above point Q, forming a 35^"o" angle QOR. Length OQ is 1, because we made it so.
<img src="/forum/uploads/imf-5036-vectors-x2.png" width="222" height="280" alt="vectors" />
OQR is a right triangle, and we are trying to find the height RQ - let's call it <i>h</i>.
So we will use
`tan 35^"o" = h/1`
Once you have that, you have your vector components in each of the <i>x</i>-, <i>y</i>- and <i>z</i>-directions, which was your original question.
If needed, your could normalize the vector OR, using the same thing we did before (divide each component by the length of OR).
Re: Vector from angle
Balder 17 Apr 2016, 07:22
Hmmm, this is just what I though as well, but looking at my spreadsheet, the number does not return the right answer.
My spreadsheet: get Right Angle - Google Sheets
Could you look to see if you may find the error?
X
Hmmm, this is just what I though as well, but looking at my spreadsheet, the number does not return the right answer.
My spreadsheet: <a href="https://docs.google.com/spreadsheets/d/1Ou7hmqn01pwAkaa4GeEq9YpX6BAwm0YNzX62Sg78TWM/edit?usp=sharing">get Right Angle - Google Sheets</a>
Could you look to see if you may find the error?
Re: Vector from angle
Murray 17 Apr 2016, 08:34
Your spreadsheet has 68^"o" for the sun's elevation, not 35^"o" as per your question.
X
Your spreadsheet has 68^"o" for the sun's elevation, not 35^"o" as per your question.
Re: Vector from angle
Balder 18 Apr 2016, 01:58
Yes, that is true. I am calculating various angles, but this should not change the result as long as the roof and solar tilt matches.
X
Yes, that is true. I am calculating various angles, but this should not change the result as long as the roof and solar tilt matches.
Re: Vector from angle
Murray 21 Apr 2016, 00:05
It's best to keep the question consistent so anyone else reading this later can follow it.
I was not aware you were trying to find the angle between 2 vectors until I saw your spreadsheet.
Maintaining the original sun vector OR (170 degrees compass, and 35^"o" elevation), and your "roof" vector ON given by (0, 1, 1), we proceed to find your required "incident" angle as follows:
(1) Find the unit vector for each of OR and ON.
They are
OR: `(-0.811, -0.141, 0.568)`
ON: `(0, 0.707, 0.707)`
they look like this:
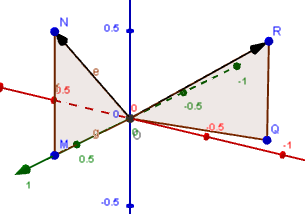
(2) Next, use the "Angle Between 3-Dimensional Vectors" on the page 7. Vectors in 3-dimensional Space :
`theta = arccos(P·Q)/(|P||Q|)`
`= arccos((-0.811xx0 - 0.141xx0.707 + 0.568xx0.707)/(1xx1))`
` = 1.264` radians
`= 74.428^"o"`
(3) I made a copy of your worksheet ("Kopy av Ark 1"), entered the values for the unit vectors OR and ON, and it successfully returned the same angle.
X
It's best to keep the question consistent so anyone else reading this later can follow it.
I was not aware you were trying to find the angle between 2 vectors until I saw your spreadsheet.
Maintaining the original sun vector OR (170 degrees compass, and 35^"o" elevation), and your "roof" vector ON given by (0, 1, 1), we proceed to find your required "incident" angle as follows:
(1) Find the unit vector for each of OR and ON.
They are
OR: `(-0.811, -0.141, 0.568)`
ON: `(0, 0.707, 0.707)`
they look like this:
<img src="/forum/uploads/imf-4803-vectors-x3.png" width="305" height="214" alt="vectors" />
(2) Next, use the "Angle Between 3-Dimensional Vectors" on the page <a href="/vectors/7-vectors-in-3d-space.php">7. Vectors in 3-dimensional Space</a> :
`theta = arccos(P·Q)/(|P||Q|)`
`= arccos((-0.811xx0 - 0.141xx0.707 + 0.568xx0.707)/(1xx1))`
` = 1.264` radians
`= 74.428^"o"`
(3) I made a copy of your worksheet ("Kopy av Ark 1"), entered the values for the unit vectors OR and ON, and it successfully returned the same angle.Re: Vector from angle
Balder 22 Apr 2016, 02:30
Dear Murray, you have written the numbers (result) into the spreadsheet, but that does not really help me.
May you write the formulas, so I may try to understand the concept?
X
Dear Murray, you have written the numbers (result) into the spreadsheet, but that does not really help me.
May you write the formulas, so I may try to understand the concept?
Re: Vector from angle
Murray 23 Apr 2016, 00:29
I think the only thing missing from your spreadsheet was the calculation for the normal of each of the vectors.
But I know you can do that already (divide each of the coordinates by the length of the vector.)
I entered numbers directly just to make sure the rest of your spreadsheet calculations were working OK.
So just set up your situation for the initial case you asked about, include the normalisation fo the vectors and it should all work OK.
that is, I believe you already had 90% of it
X
I think the only thing missing from your spreadsheet was the calculation for the normal of each of the vectors.
But I know you can do that already (divide each of the coordinates by the length of the vector.)
I entered numbers directly just to make sure the rest of your spreadsheet calculations were working OK.
So just set up your situation for the initial case you asked about, include the normalisation fo the vectors and it should all work OK.
that is, I believe you already had 90% of it
Re: Vector from angle
Balder 23 Apr 2016, 03:06
OK, thank you!
Related Vectors questions
- differentiating xihat+yjhat+zkhat. [Solved!]
How is it done in a simpler example.
(x^2+y^2+z^2) times [xihat+yjhat+zkhat divided by sqrt (x^2+y^2+z^2)] 6761hash 11 Aug 2017, 08:27
- Vectors [Solved!]
In the figure (also at http://prnt.sc/cqth0m), vector OB is three times longer than OA, BC... asad 07 Oct 2016, 07:45
- Vectors [Solved!]
In the diagram
AB = p
CA = q
... Swalay 05 Sep 2016, 06:25
- Vectors question [Solved!]
Let U,V & W be 3 vectors,which of the following make sense and which... James 18 Dec 2015, 10:39
Vectors lessons on IntMath
top







