Reuleaux triangles
By Murray Bourne, 08 Dec 2015
Here's an interesting sculpture made of Reuleaux triangles.
What are these triangles and what are they good for?
How to construct a Reuleaux triangle
We begin with an equilateral triangle PQR and draw arcs from points P, Q and R to the opposite two vertices, as follows:
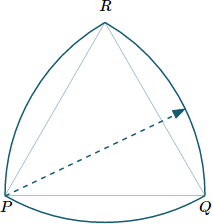
Reuleaux Triangle - step 1, extend arcs from vertices
The resulting Reuleaux triangle has quite "pointy" vertices, and we can make them more round via another step.
Extend the original triangle with equal length segments through P, Q and R as follows:
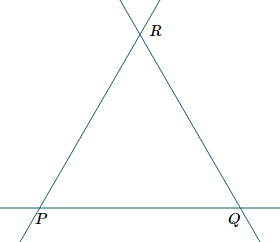
Reuleaux Triangle - step 2, extend original triangle
Next, draw arcs through the new end points, and smaller arcs at the vertices, as follows:
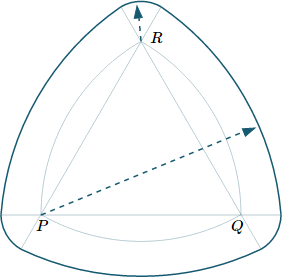
Reuleaux Triangle - step 3, extend large and small arcs
Guitar plectrum
The guitarists amongst you will recognize a guitar plectrum looks quite similar to our Reuleaux triangle:
Equal width characteristic
One of the interesting characteristics of Reuleaux triangles is they maintain equal width when rotated.
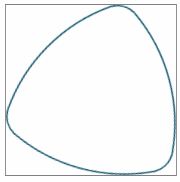
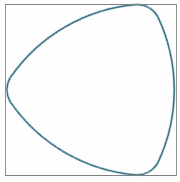
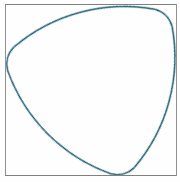
Equal width nature of Reuleaux Triangle - rotated by 15° each time
Rotary Wankel engine
First conceived in Germany in the 1920s and developed through the 1960s and 70s, the Wankel rotary engine is based on the equal diameter characteristic mentioned above. Rather than having pistons that compress gas and fire the mixture, the Wankel engine performs the same functions with less moving parts, and less weight.
I've always thought the Wankel engine was a clever design and made a lot more sense than piston engines, but it never really took off as a serious contender for the car industry. It's found some other uses in motorbikes, aircraft and more recently, Mercedes Benz has used them in the safety belt pre-tensioner system.
Other equal-width shapes
We can construct other shapes that have equal widths when rotated. Here are a few.
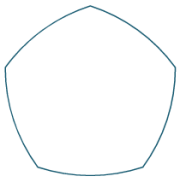
Other Reuleaux shapes based on regular pentagon, septagon and nonagon, with an irregular shaped one as well.
Bicycle with Reuleaux wheels
This Chinese invention has a triangular rear wheel and pentagonal front wheel. It needs a mechanism to separate the frame from the wheel, and it apparently takes a fair bit of extra energy to ride it, but it works.

Bicycle with Reuleaux wheels.
Onigiri
On another light note, Japanese onigiri (rice balls) are most often presented in a Reuleaux triangle shape:
Christmas tree
Being that time of the year, I made this Christmas tree entirely using multiple such triangles:

Reuleaux triangle Christmas tree.
Related article
See also the article on the Butterfly Map of the World, based on the same shape.
Be the first to comment below.



