Pi Day today (3/14) - Buffon’s Needle
By Murray Bourne, 14 Mar 2009
Today we celebrate Pi Day. The first 3 digits of pi are 3.14 and today's date, when written in the US style, is 3/14.
Some people get really carried away and have a special even at 1:59 PM, since the next 3 digits of pi are 159. However, if they were really keen, they would do it at 1:59 AM — it seems more respectful that way... 🙂
Did you realize that you can get an estimate of pi that involves probability and dropping needles on a table?
Buffon's Needle
Say you have a needle that is 5 cm long. You draw a set of parallel lines 5 cm apart on a piece of paper, and begin dropping the needle onto the paper.
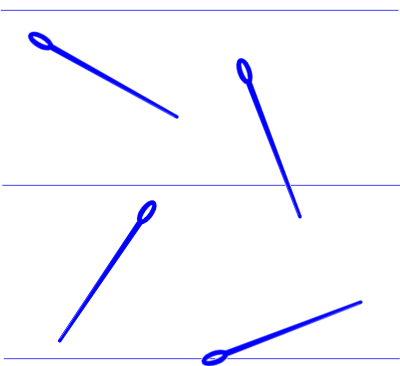
When the needle lands, it either touches one of the parallel lines, or it doesn't.
It turns out that the probability of the needle landing on one of the lines is 2/pi. From there, we can get a value of pi, as follows:
pi = (2 × the number of drops) / (number of line touches)
The problem was first posed by Georges-Louis Leclerc, Comte de Buffon in 1777.
You can see some analysis of this problem and Java applets to see how it works here: Buffon's Needle An Analysis and Simulation (which has a good explanation, but a weak applet) and here: Buffon's Needle (which has a good applet, but brief explanation).
See the 1 Comment below.
14 Mar 2009 at 4:03 pm [Comment permalink]
[...] This post was timed to be published at 1.59PM, but apparently the real Pi-Moment should be (respectfully) 1.59AM instead. Oh well … Miss Loi shall have to wait till next year to atone for her sin and [...]