The IntMath Newsletter - 10 Aug 2008

In this Newsletter:

1. Finding Square Roots - without a calculator
2. The Story of Rene Descartes
3. From the math blog
4. Math Study Tip - Time

---

1. Finding Square Roots - without a calculator

[This topic was suggested by a reader].

Mathematics is not some static stuff that comes from a textbook. It has been developed over thousands of years as a powerful tool for solving problems.

Our understanding of mathematics improves if we see how things were solved in the past.

Ever wondered how people found square roots before they had calculators? Let's look at one method that was in common use up until about 100 years ago, called the "Babylonian method".

This method involves iteration. Iteration means that we start with an approximation and substitute it into a formula. The result is a better approximation. We take that result and substitute it into our formula once more, giving us an even better approximation. We keep going until the accuracy is as good as we need.

These are the steps that we can use to find the square root of a number:

(a) Guess an answer,
(b) Divide the number by the guess, then
(c) Average the numbers in steps (a) and (b).

We can write that as a formula:

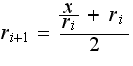
x is the number whose square root we are finding, and r_i is our guess.

Example: Find the square root of 5

A good first guess for √5 is r₀ = 3. That's step (a). Then step (b) is divide 5 by 3 then step (c) is average the resulting numbers. This is how it looks:

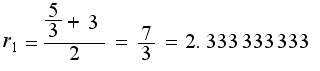
This is a better approximation. We now put that result back into our formula, giving us r₂:

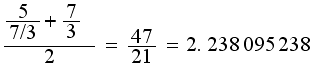
Notice that I used the fraction from the first step and not the decimal (this gives better accuracy).

Now for r₃:

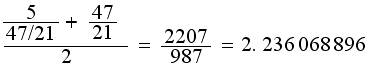
One more, r₄:

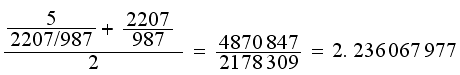
This is actually a very good approximation after just 4 iteration steps. The value is correct to 9 decimal places. Here is the first 75 decimal places of the square root of 5 (if anyone cares):

√5 = 2.2360679774 9978969640 9173668731 2762354406 1835961152 5724270897 2454105209 25638.

Iteration is an important concept in mathematics. For example, in calculus, Newton's Method is used to find roots of equations when there is no other way. Also, iteration is used in creating fractals.

A fractal image, found using iteration of complex numbers.

---

2. The Story of Rene Descartes

The brains of great people have held a fascination for scientists for hundreds of years. What kind of brain does a brilliant person have? Is it large size? Is it a special shape that makes a brain brilliant?

Rene Descartes was a French mathematician and philosopher who lived from 1596 to 1650. The owner of one of the most brilliant minds in history had a strange end - his skull disappeared.

First, let's see some of Descartes' achievements.

(a) Descartes invented analytic geometry

The "cartesian" coordinate system is named after Rene Descartes. His system of representing the relationship between 2 variables on a rectangular grid (using x- and y-axes) was an extremely valuable invention and it advanced math and science considerably.

The coordinate system was an important step leading to the development of calculus by Newton and Leibniz a few decades later.

(b) Descartes developed a theory of knowledge

The most famous quote arising from Descartes' theory is "I think, therefore I am." (or more precisely: "I doubt, therefore I think, therefore I am"). In simple English, the phrase means that if someone is capable of wondering whether or not he exists, that proves that he does actually exist.

(c) Descartes believed that the human mind (soul) was not part of the body

The implication of this view is that thinking did not go on anywhere in the body. According to Descartes, the mind interacted with the body in the pineal gland (a small blob in the brain named after the pine nut).

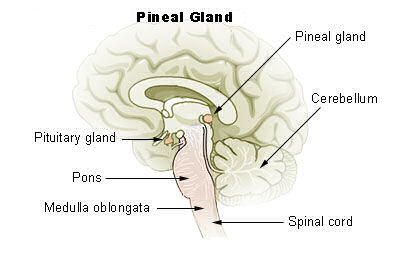
Image source.

Now we know that the pineal gland regulates melatonin, which is the hormone that regulates sleep.

Descartes believed that only humans had a soul (mind) and therefore were the only creatures that felt pain. His view led to cruel experiments on live animals. (Such experiments became common in Europe but were abandoned during the Enlightenment, 100 years later).

The Stolen Skull

In the time of Descartes in the early 17th century, very little was known about the human brain. And before that, there were many strange views about the brain.

The Egyptians thought that the brain did 'nothing important' and they believed that the heart was the center of intelligence and emotions. (This view survives to this day in sayings like "I love you with all my heart".)

The Babylonians thought all the action of mind and emotion happened in the liver. (Can you imagine saying "I love you with all my liver"?). The Greek Aristotle thought the brain was just a radiator for the body's heat.

It became common to "harvest" the brains of great people after they died as a way to answer questions like, "Do brilliant people have large brains?" and "What brain shape gives its owner the best intelligence?".

Brain researchers were a bit late to harvest Descartes' brain, but they got his skull 17 years after his death. They were shocked to find that it was quite small. Descartes' skull actually disappeared for some time and while there is a skull with his name on it in Paris' Musee de l'Homme (Museum of Man), it may not be his at all.

Most of us have brains that have a mass of about 1.3 kg. It is not so much brain mass that is important for intelligence, but the relative size of different parts of the brain. For example, Einstein's brain had larger than normal parietal lobes (the area just above and behind his ears), and it is believed that this gave him his advanced mathematical abilities.

Descartes was very important in the story of math. I wonder where his real skull ended up?

---

3. From the Math Blog

1) Changing people's lives - with math
I received a delightful mail today from a lady who lives on an isolated island off Europe. She finds Interactive Mathematics a really valuable resource for teaching her daughter mathematics and for escaping the poverty trap.

2) Friday Math Movie - Stressed Out
There have been some high profile building and bridge collapses. Can we predict such disasters and fix the structures before there is a tragedy? Math to the rescue.

3) Math rendering in WordPress using WPMathPub
How do you enter math equations, fractions and the like into a blog? One way is to use images, but these can be fiddly and inconvenient. WPMathPub is a WordPress plugin that may be a solution.

4) High fuel costs affecting learning
The rapid increase in fuel prices is forcing a re-think on educational institutions. Can we afford to (and do we really need to) transport students around our cities when there are other options, which could possibly have better learning outcomes?

5) Girls as good as boys in math - or is it something else?
A recent study shows that girls are as good as boys in mathematics. But what did the study really reveal?

4. Math Study Tip - Time

Most of us are "time-poor" and complain that there are too many things to do each day. But have you thought about how to reduce distractions and to focus more?

Here are some things to try. I guarantee they will make you more productive.

(a) Set 2 or 3 realistic goals for the day: These might include finishing a math assignment; preparing for an exam or maybe writing a paper.

(b) Don't open your email first thing in the day: Those mails can wait. Most of them are junk and distract you from your main goals. Hold off on email until you have completed your other tasks.

(c) Don't multitask: Lots of students like to have the TV on, or maybe have a YouTube video playing, or several MSN screens demanding attention. Turn them all off until the main goals of the day are achieved.

One of our most precious commodities is time. Take control of it and you start to achieve what you really want.

Here's an interesting quote:

"Watches are so named as a reminder - if you don't watch carefully what you do with your time, it will slip away from you." ~Drew Sirtors

Have a good week.

See the 10 Comments below.