Fractals

With computers, we can generate beautiful art from complex numbers. These designs, some of which you can see on this page, are called fractals.

Fractals are produced using an iteration process. This is where we start with a number and then feed it into a formula. We get a result and feed this result back into the formula, getting another result. And so on and so on...

Fractals start with a complex number. Each complex number produced gives a value for each pixel on the screen. The higher the number of iterations, the better the quality of the image

Common fractals are based on the Julia Set and the Mandelbrot Set.

Julia Set

The Julia Set equation is:

Z_n+1 = (Z_n)² + c

For the Julia Set, the value of `c` remains constant and the value of Z_n changes.

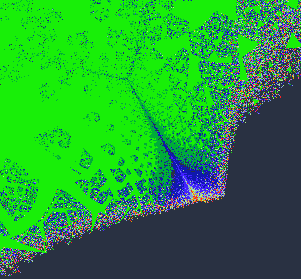
Example of a Julia Set:

If we start with the complex number Z₁= 0.5 + 0.6j, and let `c = 0.3` and then feed this into the formula above, we have:

Z₂ = (0.5 + 0.6j)² + 0.3 = 0.19 + 0.6j

We now take this new answer and feed it back in:

Z₃ = (0.19 + 0.6j)² + 0.3 = -0.0239 + 0.228j

Continuing, we find that

Z₄ = 0.24858721 − 0.0108984j and

Z₅ = 0.3616768258

− 0.005418405698j

The Mandelbrot Set

The Mandelbrot Set (discovered accidentally by an IBM computer programmer of that name) is the same as the Julia Set, but the value of c is allowed to change.

More fractals

The Fractal Fern

The "fractal fern" is generated completely by fractals. This is not a digital photograph - it is completely computer-generated.

Autumn

Image source: Fractales

Is There a Use for Any of This?

There certainly is.

A US company called Fractal Antenna Systems, Inc. makes antenna arrays that use fractal shapes to get superior performance characteristics, because they can be packed so close together.

This design ensures performance improvements in antennae used in wireless, microwave, RFID (Radio Frequency Identification) and telecommunications.

More details can be found at: http://www.spacedaily.com/news/antenna-02d.html

See also Math of the Moors.