12. Parallel AC Circuits
Recall Ohm's law for pure resistances:
`V = IR`
In the case of AC circuits, we represent the impedance (effective resistance) as a complex number, Z. The units are ohms (`Ω`).
In this case, Ohm's Law becomes:
V = IZ.
Recall also, if we have several resistors (R1, R2, R3, R4, …) connected in parallel, then the total resistance RT, is given by:
`1/(R_T)=1/R_1+1/R_2+1/R_3+...`
In the case of AC circuits, this becomes:
`1/(Z_T)=1/Z_1+1/Z_2+1/Z_3+...`
Simple case:
If we have 2 impedances Z1 and Z2, connected in parallel, then the total resistance ZT, is given by
`1/(Z_T)=1/Z_1+1/Z_2`
We can write this as:
`1/(Z_T)=(Z_2+Z_1)/(Z_1Z_2)`
Finding the reciprocal of both sides gives us:
`Z_T=(Z_1Z_2)/(Z_1+Z_2)`
Example 1
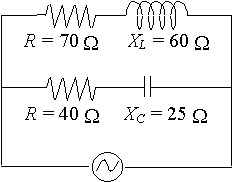
Find the combined impedance of the following circuit:
Answer
Call the impedance given by the top part of the circuit Z1 and the impedance given by the bottom part Z2.
We see that Z1 = 70 + 60j Ω and Z2 = 40 − 25j Ω
So
`Z_T=(Z_1Z_2)/(Z_1+Z_2)`
`=((70+60j)(40-25j))/((70+60j)+(40-25j))`
`=((70+60j)(40-25j))/(110+35j)`
(Adding complex numbers should be done in rectangular form.
Now, we convert everything to polar form and then multiply and divide as follows):
`=((70+60j)(40-25j))/(110+35j)`
`=((92.20/_40.60^text(o))(47.17/_-32.01^text(o)))/(115.4/_17.65^text(o))`
(We do the product on the top first.)
`=((92.20xx47.17)/_(40.60^text(o)-32.01^text(o)))/(115.4/_17.65^text(o))`
`=(4349.074/_8.59^text(o))/(115.4/_17.65^text(o))`
(Now we do the division.)
`=(4349.074)/115.4/_(8.59^text(o)-17.65^text(o))`
`=37.69/_-9.06^text(o)`
(We convert back to rectangular form.)
`=37.22-5.93j`
(When multiplying complex numbers in polar form, we multiply the r terms (the numbers out the front) and add the angles. When dividing complex numbers in polar form, we divide the r terms and subtract the angles. See the Products and Quotients section for more information.)
So we conclude that the combined impedance is
`Z_T = 37-5.9j\ Omega`
Example 2
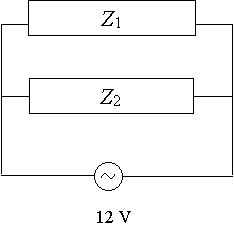
Given that Z1= 200 − 40j Ω and Z2= 60 + 130j Ω,
find
a) the total impedance
b) the phase angle
c) the total line current
Answer
a) `Z_T =frac{Z_1Z_2}{Z_1 + Z_2}`
`=frac{(200-40j)(60+130j)}{(200-40j)+(60+130j)} `
`=frac{(200-40j)(60+130j)}{260+90j}`
`=frac{(204.0angle-11.31^@)(143.2angle65.22^@)}{(275.1angle19.09^@)}`
`=frac{204.0times143.2}{275.1}angle(-11.31^@+` `65.22^@-` `{:19.09^@)`
`=106.2angle34.82^@`
`=87.18+60.64j`
So we conclude that the total impedance is
`Z_T = 87.2+60.6j\ Omega`
b) We see from the second last line of our last answer that
the phase angle is `~~35^@`.
c) Total line current:
We use
- V = IZ,
- the fact that the impedance is `106.2 ∠ 34.82^@` and
- the fact that the voltage supplied is `12 V = 12 ∠ 0^@\ V.`
So
`I = V/Z`
`=frac{12angle0^@}{106.2angle34.82^@}`
`=0.113angle-34.82^@ "A"`
Example 3
A `100\ Ω` resistor, a `0.0200\ "H"` inductor and a `1.20\ mu"F"` capacitor are connected in parallel with a circuit made up of a `110\ Ω` resistor in series with a `2.40\ mu"F"` capacitor. A supply of `150\ "V"`, `60\ "Hz"` is connected to the circuit.
Calculate the total current taken from the supply and its phase angle.
Answer
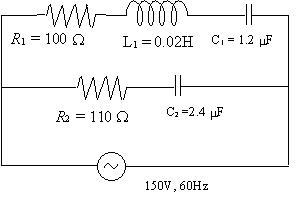
For Z1 (the upper part of the circuit), we have:
XL = 2πfL = 2π (60)(0.0200) = 7.540 Ω
`X_C=1/(2pi(60)(1.20xx10^-6))`
`=2210.485\ Omega`
Z1 = R1 + j(XL − XC)
= 100 + j(7.540 - 2210.485)
= 100 − 2202.9j
`= 2205.21 ∠ − 87.40^@\ Ω`
For Z2 (the lower part of the circuit), we have:
`X_C=1/(2pi(60)(2.40xx10^-6))`
`=1105.243\ Omega`
Z2 = R2 + j(XL - XC)
= 110 + j(−1105.243)
`= 1110.7 ∠ −84.32^@\ Ω`
So the total impedance, ZT, is given by:
`Z_T=(Z_1Z_2)/(Z_1+Z_2)`
`=(2449326.75/_-171.72^"o")/(210-3308.188j)`
`=(2449326.75/_-171.72^"o")/(3314.85/_-86.37^"o")`
`=738.9/_-85.35^"o"`
This last line in rectangular form is ZT = 59.9 − 736.5j Ω
Now:
`I_T=(V_T)/(Z_T)`
`=(150/_0^"o")/(738.9/_-85.35^"o")`
`=0.203/_85.35^"o"`
So the total current taken from the supply is `203\ "mA"` and the phase angle of the current is `~~85^@`.