IntMath Newsletter: Wu’s squaring trick, PatrickJMT, Google calculus
By Murray Bourne, 27 May 2014
27 May 2014
In this Newsletter:
1. Wu's squaring trick
2. Resource - PatrickJMT math videos
3. Google uses integration to speed up the Web
4. Volunteers wanted!
5. Math puzzles
6. Friday math movie: 5 Quick Math Tricks for Filmmakers
7. Final thought - walking and problem solving
1. Wu's squaring trick
Here's a neat number trick, attributed to Scott Wu, that could be a good one to impress people at your next party (depending on your social group, of course...).
You can quickly square numbers over 25 in your head. It uses this identity:
n2 = (n − 25) × 100 + (n − 50)2
For example,
622 = 37 × 100 + 122 = 3844
442 = 19 × 100 + 62 = 1936
Can you see how it works?
[Source: Wu's Squaring Trick, Quora]
2. Resource - PatrickJMT math videos
 |
I came across Patrick JMT math videos recently. His tagline is:
|
The extensive list of videos cover basic number and algebra, through logarithms, trigonometry and probability, to calculus.
These JMT videos are similar in style to the Khan Academy offerings, but I find them easier to follow because they're easier to watch (no black background). They are "over the shoulder"-type videos where you can see all the steps, and include plenty of examples.
The "JMT" stands for "just math tutorials".
The link again: Patrick JMT math videos
3. Google uses integration to speed up the Web
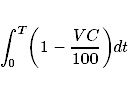 |
Google tries hard to provide super-fast Web pages, and uses calculus in the process. They want everyone else to produce fast pages as well. See how integral calculus is involved. |
4. Volunteers, please!
I have a small task that some of you may be interested in - and you could learn something from it, too.
I made 6 short videos about integration some time ago and I need some help to transcribe the soundtrack of the videos. It just means typing out the text of my commentary.
The sound quality is not very good on those videos (they were made using Flash and then converted for YouTube) and I hope to record the soundtrack again. In the meantime, the transcription will help users to follow what is going on.
If you are studying calculus now, or will be soon, (or are just interested), this is a good opportunity to learn some of basic calculus concepts while helping me out.
If you would like to be involved, please reply to this email, or reply in the comment box.
5. Math puzzles
The puzzle in the last IntMath Newsletter asked you to find the intersection of a pulley belt with one of its wheels.
Correct answers with explanation were given by Colin, Nicos, Tomas and Don.
New math puzzle: Brigitte and Ric are sitting on their motorbikes at a rest stop beside a busy a interstate highway. They observe that the cars can be partitioned into three types, fast (120 km/h), medium (90 km/h) and slow (60 km/h). They also observe that one of each type passes every 10 seconds.
Brigitte remarks that since she always travels at 90 km per hour she can expect to overtake and be overtaken by equal numbers of cars. Ric says "nonsense", and they agree on the following bet.
Ric will pay Brigitte $1.00 for every car that overtakes her before the next rest stop if she pays him $1.00 for every car she overtakes. The next rest stop is 90 kms away.
Who wins, and by how much?
Leave your responses here.
6. Friday math movie: 5 Quick Math Tricks for Filmmakers
 |
This short video from Indy Mogul discusses some of the math involved in making videos. There are many connections between the arts and math! |
7. Final thought - walk to solve problems
I've been doing a lot of programming lately, mostly re-writing the old Flash-based math applets on IntMath so they're mobile-device friendly.
Programming involves a lot of problem solving, where things often don't work as expected, or not at all. It can involve staring at the screen for long stretches, trying to get to the bottom of the issue.
I find one of the best problem-solving methods is to go for a walk. It's amazing how you can see things more clearly, and see the broader picture when away from the screen. Walking also increases your blood flow, and that's essential for good brain functioning.
So next time you're stuck on a math problem, go for a short walk. It will help your mental and physical health, and hopefully give you the insight you need.
Until next time, enjoy whatever you learn.
See the 9 Comments below.
27 May 2014 at 9:47 pm [Comment permalink]
I looked at the first Patrick video on exponents. 3*3*3*3*3= 3^5. Then he immediately gives the identity (a^m)*(a^t) =and I quit after that. This is "typical" teaching, where the teacher tells the student everything, assuming the student knows nothing. I am in the process of showing teachers how this should be done. All of my teaching involves getting my students to look for patterns, to ask questions, to change things... Murray, I'll send some things on Logs that I do: last week this 7th grader, after she found log(a^b)=b*Log(a), from the data, she told me that log(a)/log(sqrt(a)) = 2 is an identity. I never saw that before! When the kids are asked to make up the identity, I learn things.
28 May 2014 at 9:44 am [Comment permalink]
@Don: This is one of the limitations of any kind of pre-recorded lesson. You don't have the opportunity to prompt students, gauge their response, ask other probing questions and then let them discover.
I agree that is the best approach, but for videos, it's not so easy.
However, I designed an online course recently that used video which would pause and ask students a question. It's a good compromise, I think.
For those without a text book, (or who struggle to follow a text book), the Patrick videos (and Khan, and the MathTutorDVD ones) do have a place and value.
28 May 2014 at 10:09 am [Comment permalink]
Assume that at time t = 0 a fast car goes through the starting point (d = 0) and that Birgitte starts her trip at that very moment, attaining her cruising speed almost immediately. At time t = 40 sec she will be be at a distance d = 1 km. But the second fast car (120 km/h) passed the origin at time t = 10 sec, and took 30 seconds to travel 1 km, so that at time t = 40 it will be at point d = 1 km, same as Brigitte. 40 sec later, i.e., at time 80 sec, she reaches the point d = 2 km. The third fast car passes the origin at time t = 20 sec, and will take 60 sec to get to point d = 2 km, that is, 80 sec altogether.
The situation repeats itself over and over, so that a fast car passes Brigitte every 40 seconds, which means that she will be overtaken 90 times up to and including the next stop, one hour away.
Now look of the successive positions of Brigitte at times t = 20, 40, 60,...; these positions are, respectively, d = 0.5, 1, 1.5,... After Birgitte departs, the first slow car (60 km/h) going through d = 0 will be at d = 0.5 km when t = 20 sec; the second one will be at d = 1 km at t = 40 sec, and so on. These are the overtaking moments, i.e., 3 per minute. So, in an hour Brigitte will overtake 180 slow cars during the hour up to the next stop.
Ric has to pay Brigitte $90, and she has to pay Ric $180, which leaves her on the losing side by $90.
28 May 2014 at 9:28 pm [Comment permalink]
The answer is Brigette loses the bet by 90 dollars.
Explanation:
Let’s consider there are three roads for these three types of cars. If we start the time t from t=0 sec. with three cars at Rest shop 1, we can observe for every 10 seconds the same pattern occurs in terms of positions with one car entering the road at Rest shop 1 and one car leaving the road at Rest shop 2 i.e. one car advancement in all three roads. I think I have explained clearly.
Now, there are totally 540 positions of 60kmph cars between Rest shops 1 and 2. Similarly, 360 and 270 for 90kmph and 120kmph cars respectively.
It takes 1 hour for Brigette to reach shop 2. After 1 hour i.e. at t=3600 sec.
The distance of separation between Brigette and the first 60kmph car = 30km
The distance of separation between Brigette and the first 120kmph car = 30km
Formulae:
Number of cars overtaken by Brigette = the number of positions in between current Brigette’s position and current position of the first 60kmph car (which has started along with Brigette at shop 1) = number of positions on 60kmph road in 30km = 180
Number of cars that have overtaken Brigette = the number of positions in between current Brigette’s position and current position of the first 120kmph car (which has started along with Brigette at shop 1) = number of positions on 120kmph road in 30km = 90
So Brigette got 90 dollars but lose 180 dollars. So she has lost the bet by 90 dollars.
29 May 2014 at 8:43 pm [Comment permalink]
video is somehow challengeable to me.if possible i like posted quations from calculas and analytic mathematics beginning with introduction together with their answers.otherwise i like maths since solving a math tasks is solving life challenges
29 May 2014 at 9:11 pm [Comment permalink]
Wu's squaring trick is very interesting! Only problem is I would need another trick to use it. It's as hard as trying to do it the old fashion way. 🙁
30 May 2014 at 1:00 am [Comment permalink]
Let t be the current time, such that t=0 be the time at which Ric and Brigitte start cruising at exactly 90 km/h.
Let D (Delta) be the time at which other cars pass by their rest stop. The assumption here is that all three types of cars will pass by the rest stop at the exact time.
The equations of the cars are as follows:
distance = speed * (t - D).
UNITS:
Let t be in tens of seconds, such that Ric and Brigitte will get to their second stop, which is 90 km/h away, in 360 t's. then, speeds will be 90/360 for medium, 120/360 for fast and 60/360 for slow. By imposing D to be integers, we make cars start at 10 second intervals, and it's easier to discretize our problem this way.
MAX AND MIN:
What we try and do next is find what's the latest a fast car can leave the rest stop to overtake Brigitte. We know that Brigitte can never overtake a fast car.
This is can be characterized in the following system of equations:
y = 90 at final overtake possibility
y = (90/360)t --> t = 360
y = (120/360)(t - d) --> d = 30*360/120
which means d = 90 t's, or 900 seconds. Brigitte is overtaken 90 times.
What we also try and find is find the earliest time a slow car can leave the rest stop to be overtaken by Brigitte. Using a similar system of equations, we get d = -180, which means that the cars have to leave 1800 seconds earlier than Brigitte so that they can still be overtaken by her.
Ric will pay Brigitte 90$ and Brigitte will pay Rick 180$. Ric obviously wins.
PS: this solution assumes that the cars leave in packs of 3 from the rest stop at different speeds.
16 Jun 2014 at 2:52 pm [Comment permalink]
As I view all of the lessons presented by this website, I was really amazed not just because it is very helpful in my studying but it also enlightened my mind on the different aspects of mathematics.. Hoping that this will continue to serve us..
16 Jun 2014 at 5:36 pm [Comment permalink]
@Raymond: I'm glad you find IntMath useful!