IntMath Newsletter: Eigenvectors, 3D solar system, graphics
By Murray Bourne, 30 Jul 2019
30 Jul 2019
In this Newsletter:
1. New on IntMath: Eigenvalues and eigenvectors
2. Resources: Desmos and 3D simulator
3. Math in the news: News and science
4. Math movies: Graphics and addresses
5. Math puzzle: Tangent circles
6. Final thought: Culture
1. New on IntMath: Eigenvalues and eigenvectors
Eigenvectors are very important in many science and engineering fields, including compuer science. (Google's search algorithm is based on eigenvectors.) It was one of the many topics I learned about as a math student where I could find the answers, but I really had no idea what I'd found, what the concept really meant, or what they were good for.
I wrote some new pages incorporating interactive applets which I hope gives the reader a better idea of what this interesting topic is all about. (It's usually taught at university level, but the mathematics involved is not that challenging - mostly multiplying and adding.)
 |
On this page we see how multiplying by a matrix can achieve the kind of transformations graphics artists and robot designers use a lot, including reflection, rotation, skew (shear), scaling and displacement. |
The applet on this next page allows you to explore the physical meaning and geometric interpretation of eigenvalues and eigenvectors.
 |
I've used stretching of a map of my home country to show how transformations achieved by matrix multiplication can be replaced with much simpler scalar multiplication (which is a key idea of this topic). |
Like most matrix operations, it's very easy to make simple mistakes when calculating eigenvalues and eigenvectors.
 |
This calculator allows you to check your work, and/or to explore what happens with eigenvectors for everything from 2x2 and 3x3 up to 9x9-size matrices. |
You may also be interested in:
How to find eigenvalues and eigenvectors? (outlining the algebraic steps for finding them - this was the only part I learned at university).
Applications of eigenvalues and eigenvectors (which includes a highly simplified description of how Google search works).
2. Resources
(a) Using Desmos to create learning resources
Here's a recent tweet by teacher Liz Caffrey:
 |
Check out how one of my students uses the graphing calculator to take notes! She sets up and saves a new graph each day. Here are her notes from our notice/wonder on standard form of quadratics! I never would have thought of doing this. |
I know from my own experience how much richer my understanding of topics is after I've created similar interactive explorations. Doing it with Desmos is really quite easy, and I encourage you (whether student or teacher) to give it a go. You don't need a lot in the way of programming skills.
(b) Harmony of the spheres
This is a 3D simulation of the solar system, built on an "open source gravity simulator".
It also has some "What-if" scenarios. This example shows what would happen if Earth actually orbitted Saturn:
 |
You can drag left-righ, up-down to explore and use the mouse wheel to zoom. Press the "Play" button at the top to animate the scene. |
You can also change the physics parameters, and add masses. It's very nicely done. (Probably best on a laptop.)
3. Math in the news: News and science
Last week marked the 50th anniversary of the moon landings. This was an extraordinary human achievement, but the misguided belief that it was all a hoax continues to grow, fuelled by ignorant people (and bots) through social media. Where and how we find our news, and how we critically examine the sources and conclusions, becomes increasingly important as the growth of fake news has the potential to rip apart our societies.
(a) How do we find out what's happening?
In the US, more people get their news from social media than traditional news sources, while in other countries it's the reverse. See a short summary: Where do people find news on their smartphones?
From the original Digital News Report, by Reuters and University of Oxford: Executive Summary and Key Findings of the 2019 Report
(b) What do we know about science?
Those of us involved in science education would like to think most students graduate with a reasonable general knowledge of the various branches of science, and will have a good grounding in how science actually works. But it appears that is not always the case.
The (US) National Science Board's Science and Engineering Indicators 2018 makes for some sobering reading.
Science and Technology: Public Attitudes and Understanding
Here's a sample of the misunderstandings gleaned from the results of various quizzes.
- Antibiotics kill viruses (which is false): 50% or more got it wrong in most countries
- Human beings developed from earlier species of animals (true): 30 to 50% got it wrong
- Astrology is scientific (false): around 40% (US) thought it was true
- Understanding experimental design: over 50% got it wrong in most countries
No wonder we have the growth of drug-resistant superbugs, rampant species destruction, and climate change deniers.
4. Math Movies
(a) The simple genius of a good graphic
 |
Data visualization is an increasingly important item in everyone's skill set these days. Information designer Tommy McCall outlines the evolution of charts and diagrams with plenty of interesting examples. |
(b) A precise, three-word address for every place on Earth
When I first arrived in Japan where I lived for 4 years, I was amazed at how different their address system was compared to what Iwas used to. Rather than sequential numbers (usually odd on one side and even on the other) along roads, the Japanese system is built around regions and sub-regions of a suburb.
So I found the pretext of this next talk quite interesting.
 |
Many houses do not have any kind of address system, and to find anyone, you need to rely on local knowledge. Chris Sheldrick has an interesting solution - use three-word addresses! |
I like the basic concept, but surely numbers are more universal? Wouldn't addresses based on latitude and longitude make more sense, especially as that's how our phones know where we are already?
5. Math puzzles
The puzzle in the last IntMath Newsletter asked about the possible dimensions of 2 pencils.
A correct answer with sufficient reasons was submitted by Georgios. Special mention to Nicola who worked on a generalized solution involving circles and ellipses, which she explored using Desmos.
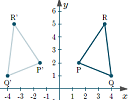
New math puzzle: Tangent circles
Circles that are "mutually tangent" touch at one point only. We have 3 such circles, with centers P, Q, R and radii p, q, r respectively. We are given the lengths PQ = 15, QR = 21 and PR = 14. Find p, q and r.
You can leave your response here.
6. Final thought - culture
Pangolin (image credit)
Living in different countries gives you fresh insights about culture. A lot of the cultural practices that seemed vital to our existence have faded as time goes on, and others we question due to their environmental impacts. While they may not have had much effect hundreds of years ago when there were less people in the world, perhaps some aspects of the following don't make a lot of sense any more?
- Buying SUVs for suburban runabouts
- Living in large houses a long way from work
- Eating whale meat
- Burning paper in the Hungry Ghost Festival
- Consuming rhino horn, pangolin scales and shark fin
- Buying ivory carvings
- Wearing baby seal furs
Maintaining the traditions while minimizing their impacts is surely the best way to move forward.
Until next time, enjoy whatever you learn.
See the 13 Comments below.
