Cookie jar math
By Murray Bourne, 29 Mar 2010
Kuih bangkit is an Asian (more specifically, Nyonya) sweet made from flour, coconut milk, egg, sugar and vegetable oil.

I was struck by how neatly the cookies were arranged in the red-topped plastic container. (These are ubiquitous in SE Asia.)

There are 10 pieces in each outer row.

There is some interesting mathematics behind neat packaging, called tessellation.
We know that bees are quite mathematically clever. Their honeycombs use a hexagon shape since it gives them the largest possible space with least amount of wax, while also being able to pack them together with no dead space remaining. This is called tessellating.
Tessellations is an important area of mathematics and has wide applications in the packaging industry, as well as in tiling and carpets.
Back to the Cookie Container
So how did the kuih bangkit bakers decide on the best size for their cookies?
Either they ordered the plastic containers to suit or they made the cookies the correct size to fit existing containers. Let's assume it's the latter (for the purposes of this mathematical discussion).
The container is 10.5 cm across, so its circumference is
10.5 × π = 33.0 cm.
The simple solution would be to make each cookie 3.3 cm across (so we can fit 10 around the edge), but that wouldn't work. Each cookie is 1 cm thick, and we need to allow for that.
The inner diameter of the cookies will be 2 cm less than the outer diameter (1 cm on each side).
The inner circumference will be
8.5 × π = 26.7 cm
So we need to make the cookies 2.7 cm across.
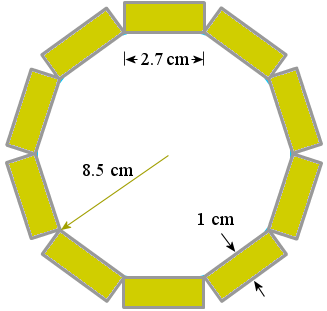
The inner radius is 8.5 cm and the outer radius is 10.5 cm. The above image is drawn to scale. You can see that a width of 2.7 cm works.
Indeed the cookies are 2.7 cm wide:

See more on Tessellations.
See the 5 Comments below.
31 Mar 2010 at 6:29 am [Comment permalink]
I know similar light and airy sweets (without the coconut milk, which would be a nice variation), available here -- freshly made! -- in non-tesselated arrangements such as in plastic bags or trays.
I'm intrigued: Do *people* pack the external wall layer of sweets onto the inside wall of the jar -- without it tumbling down? Do they use a cardboard cylinder or such to keep the outer arrangement in place until the rest of the fill is poured in? Or is it done by machine?
Loved the break from work!
3 Apr 2010 at 5:21 pm [Comment permalink]
Hi Fernando. yes, the coconut really makes the difference. ^_^
I'm not sure if they are packed by machine but it actually is not so difficult. You would pack about 3 or 4 around the edge, then pack the next layer and then one more. Then you would turn the container around about 90° and do another few. The inner layers stop the outer layer collapsing when it is at the top.
10 Apr 2010 at 3:43 am [Comment permalink]
it is very intersting topic,
but in the second step finding the perimeter of the inner space,how can we use circle formula to find perimeter of decagon?
and the cookie is irregular shape (i.e it is thicker in the center)lets say we did the first row but how can we fill the hole container by using maths?
10 Apr 2010 at 10:42 am [Comment permalink]
Hi Selemawit. I'm using a circle to approximate the inner perimeter. As this is not precision engineering, it is OK to use 1 cm as the (consistent) thickness of the cookie.
You last question is a good one. You can see from the photo that they packers tried to include as many cookies per row as possible, but it is inevitable there will be some empty spaces.
23 Aug 2011 at 4:51 am [Comment permalink]
Not only does it save space, but it must be structurally amazing as well. There isn't a crushed cookie in the entire container!