When zombies attack - a mathematical model

The authors of WHEN ZOMBIES ATTACK!: MATHEMATICAL MODELLING OF AN OUTBREAK OF ZOMBIE INFECTION are (kind-of) serious. As the researchers from The University of Ottawa say in their paper:

This is, perhaps unsurprisingly, the first mathematical analysis of an outbreak of zombie infection. While the scenarios considered are obviously not realistic, it is nevertheless instructive to develop mathematical models for an unusual outbreak. This demonstrates the flexibility of mathematical modelling and shows how modelling can respond to a wide variety of challenges in ‘biology’.

They describe a scenario containing 3 classes of beings, where "susceptibles" can become deceased through ‘natural’ causes, i.e., non-zombie-related death. The "removed" class consists of individuals who have died, either through attack or natural causes. Humans in the removed class can resurrect and become a "zombie".

Their model uses differential equations (a form of higher calculus), matrices and determinants (including eigenvalues and Jacobians). and various feedback loops to model what happens when zombies attack.

One of the scenarios (in which a "cure" for zombie-ism has been found) is graphed as follows:

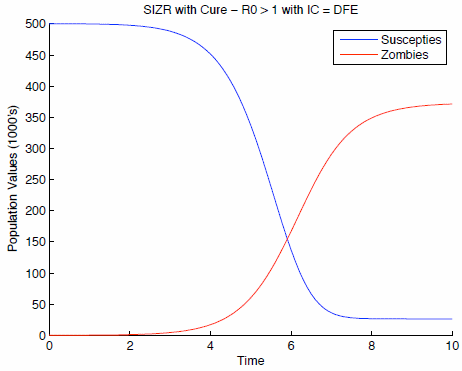
The graph shows that over time, the number of zombies levels off and the number of humans drops, but they don't completely disappear.

The researchers have used MATLAB to produce their model, and they include the code at the end of their article.

That link again: WHEN ZOMBIES ATTACK!: MATHEMATICAL MODELLING OF AN OUTBREAK OF ZOMBIE INFECTION (PDF, 18 pages)

See the 4 Comments below.