The locus and the ellipse
By Murray Bourne, 17 Jun 2008
A reader in Chile shared a great story with me recently.
Raul is 85 years old, and for over 60 years he's been bugged by a question that his professor asked him during an oral examination. I'll let Raul tell his story, which shows cool evidence of Web-savviness.
In late 1941, in an oral exam, my distinguished Professor Don Raul Valdivieso, raised the following issue:
"Find the locus of the centre of an ellipse that moves tangent to the positive x- and y-axes."
After brief reflection, I remembered a problem posed in Course Geometry Plana (year 1940) by the eminent Professor Don Luciano Claude which read as follows:
"Find the locus of the point where two straight orthogonal lines intersect, and which are tangential to a given ellipse."
The solution to this problem, easy to find in any treaty on conics, is a concentric circle to an ellipse given with the radius equal to:
√(a2 + b2), where a and b are the semi-axis of ellipse.
Explanation: "Orthogonal" means "at right angles" and as we move the pair of orthogonal lines around the ellipse so that they touch the ellipse at one point (they are tangents), a circle is formed by the intersection point:
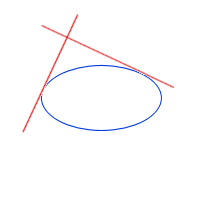
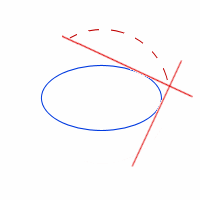
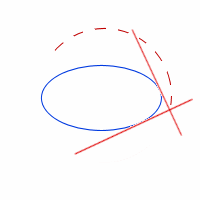
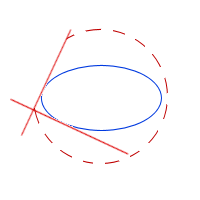
Here's the resulting circle, which is concentric with the ellipse (this means it has the same centre).
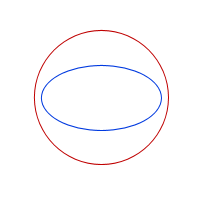
Back to Raul's story:
So it is easy to deduce that the inverse of this problem is to consider the orthogonal straight tangents as fixed and the ellipse given as mobile, returning to the problem of Professor Valdivieso.
Clearly the locus will be a portion of the arc of a circle.
However, Professor Valdivieso, even accepting that this was a good solution, required me to follow the long road, namely the analytic geometric deduction directly as initialy requested.
Result: I was not able to find such a solution.
The years passed and my attempts were in vain to find a solution following the method that I had being requested. Several colleagues whom I consulted could not resolve it.
So, already retired and close to fulfilling 85 years, I went back to this issue. The Google Scholar was no help to find what I was are looking for. Finally, using the Central Library at the Catholic University and recalling those old fragile, but extraordinary French books, I found what I was looking for in Lecons de Géométrie analytique. Author: Charles Roguet. Edition year 1860. Page 218.
We need to resolve the previously stated locus,to develop:
SECTION (A) the equation of a tangent line to the ellipse and
SECTION (B) The equation of the distance from a given point to a given straight line.
What follows is quite a lengthy analysis using the characteristics of conic sections.
So dear Reader, can you solve it given the hints above?
The final result is the red arc that you see in the following diagram (the yellow and green curves are not relevant to this problem, even though they are interesting):
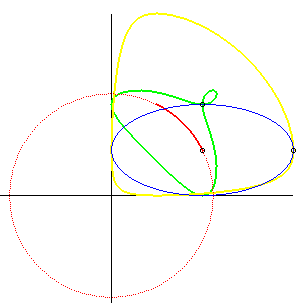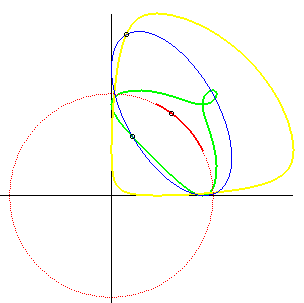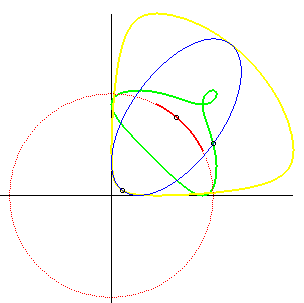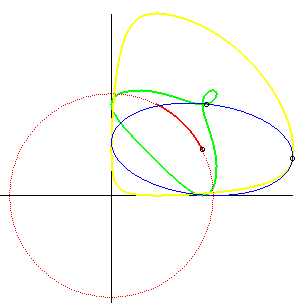
Image source: MathCurve.
Raul finished his note as follows, with a challenge to find a simpler solution than his 4 pages of algebra:
That was it. To this day I can not explain that Professor Raul Valdivieso expected that any students could develop this problem, in an examination or in any other circumstance.
It there a much simpler solution? I venture to think there has to be one, because the distinguished professor was very demanding but very thoughtful and fair.
Raúl Espinosa Wellmann, Civil Engineer, Pontificia Universidad Católica de Chile.
Thanks, Raul for the interesting story and for the evidence that a well-crafted problem is simple to state, and motivating for years.
Update: A reader asked for the full solution, and so here you go. I think you'll agree it is quite an extraordinary question for an examination!
Locus of an ellipse [MS Word document]
See the 3 Comments below.
8 Mar 2009 at 11:17 pm [Comment permalink]
Estimado Raúl:
Le contesto en mi idioma natal (soy uruguayo), y también intentaré traducir todo al inglés
Me encantó el problema planteado por usted, y le comento que encontré una solución no demasiado complicada. Para poder enviársela en forma detallada necesito la posibilidad de adjuntar archivos con otro formato distinto del texto (por ejemplo .doc, .pdf o .html).
Translation:
Mr. Raul:
I found your problem very interesting, and I would like to send you a solution which I think is not too much complicated.
In order to send you a detailed solution I need to have the possibility of attaching files of formats other than plain text; that is: .doc, .pdf or .htm.
En líneas generales, el método es:
1. Plantear la ecuación de una elipse con centro (0,0) y ejes oX y oY.
2. Rotar los ejes de la elipse un ángulo ?tita? (sin mover el centro).
3. Mover el centro de la elipse hacia (xo,yo) sin rotar los ejes.
4. Expresar las dos ecuaciones que aseguran la tangencia de la elipse con los ejes coordenados.
5. Desarrollar los cuadrados y simplificar lo más posible (esta es la parte con cálculos más engorrosos)
xo^2 = a^2.cos^2(tita) + b^2.sen^2(tita)
yo^2 = a^2.sen^2(tita) + b^2.cos^2(tita)
6. Al eliminar el parámetro ?tita? queda la condición que deben cumplir xo,yo para que se verifique la tangencia. O sea, la ecuación del lugar geométrico en variables xo,yo.
Translation:
The method is, approximately:
1. Equation from an ellipse with center at (0,0) and axis oX y oY.
2. Rotate the major axis “a” an angle θ (without moving the center).
3. Move the center of the ellipse to the point (xo,yo) maintaining the inclination θ of the major axis.
4. The ellipse must be tangent to both coordinate axis: that gives two equations with variables xo,yo and parameter θ.
5. Expand the squares: this is the most complicated part, but in the end we manage to clean a lot of terms.
xo^2 = a^2.cos^2(θ) + b^2.sin^2(θ)
yo^2 = a^2.sin^2(θ) + b^2.cos^2(θ)
6. We end up eliminating the parameter θ between the two equations:
What remains is the relationship that must be held between xo and yo in order to verify the conditions of tangency. That is the equation of the locus.
Muchas gracias por su atención.
Saludos,
ING. DIEGO SAEZ, Montevideo, Uruguay.
Translation:
Thank you very much for your attention,
Diego Saez (Engineer).
Montevideo, Uruguay.
--------------------------------------------
9 Mar 2009 at 9:17 am [Comment permalink]
Thank you, Diego Saez, for your solution (and for providing the English translation).
10 Mar 2009 at 10:02 am [Comment permalink]
Diego sent me his full solution in a MS Word document. Here it is:
Locus and ellipse solution
Thank you for taking the trouble, Diego!