Arc length for the inner curve of a window
By Murray Bourne, 06 Jan 2010
A reader who works for a glass company (true story) wrote to me recently and asked how to solve the following.
I've got to make a window with a curved top. The width of the frame is the same all round, including the part around the curved portion.
What's a formula for the length of the inner arc of the curved portion?
The required length is labeled HI in the diagram.
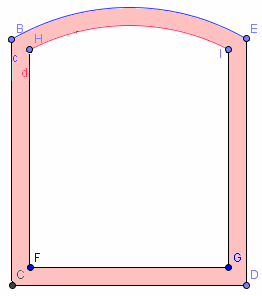
(This is not quite a "Norman window", since it's not a semi-circle on top.)
This is a typical "real life" question, in that we don't have a lot of information to go on, so we'll need to make some assumptions.
Solution - Example
Let's consider a plausible example first. We assume the curves are arcs of circles. (They looked circular in the question. If they are not circles we could adjust later, but for the sake of the example, we'll stick to this reasonable assumption.)
Let the total frame (length CD) be say 4 units wide and the edges of the frame be 0.3 units wide. I pick a point P in the center (horizontally) of the frame (I choose point P (2,1)), and draw 2 concentric circles, 0.3 units apart. The outer one is 5 units, the inner one 4.7 units. I could have chosen any radii for my concentric circles, of course, as long as the inner and outer radii differ by 0.3 units.
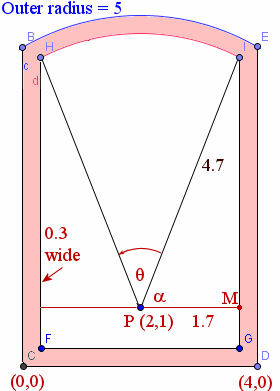
If I can find angle θ, it will be straightforward to find the arc length HI.
First, we find angle α by using the right triangle PMI.
cos α = 1.7 / 4.7 = 0.3617
Using the inverse ratio, we get that
α = arccos (0.3617) = 1.2007 (radians, of course. If we need degrees, it equals 68.79°)
[Why radians? They are more commonly used in science and engineering than degrees, and are best for this problem. For more, see Radians.]
Now we observe that 2α + θ = π (180°), since they lie on a straight line.
So angle θ = π - 2 × 1.2007 = 0.7402
To find the arc length HI, we just apply the arc length formula
s = r θ
(See arc length formula)
s = 4.7 × 0.7402
= 3.4789
So the required arc length is 3.48 units (correct to 2 decimal places).
General Solution
Let the total width (window and frame) = 2x, giving x for half the width.
Let the edges of the frame have width w.
The circles have radius R (outer) and r = R - w (inner).
Angle α = arccos ((x - w) / r)
Angle θ = π - 2 α (in radians)
Arclength HI is given by
s = r θ
= r × (π - 2 (arccos ((x - w) /r)))
This is the formula required by the glass manufacturer.
See the 13 Comments below.
6 Jan 2010 at 10:51 pm [Comment permalink]
Murray --
Thanks for the help with this formula.
Your solution is much cleaner than the lengthy solution I came up with. Implementing an efficient formula will "lean" out the process of implementing this new product into manufacturing.
Thanks again!
7 Jan 2010 at 6:43 am [Comment permalink]
You're welcome, Steve! Glad I could help.
7 Jan 2010 at 6:31 pm [Comment permalink]
Murray
This is a lovely problem.
But won't P be the intersection of BH and EI?
How do you measure the width of an arc (frame)? Will BH also equal 0.3 units?
I would love to give this problem to my students. But I think that they will want to pin point P, meaning giving a bit more information?
7 Jan 2010 at 9:15 pm [Comment permalink]
Hello Rika. Normally we draw the diagram for the question so that it is not to scale (so students really need to think it through).
But for both the first and second diagrams above, I have actually drawn them to scale. Some careful observation will indicate that P is not the intersection of BH and EI. It could be of course, but only for one inner radius.
BH does not equal 0.3. The extension of PH to the outer radius will give a segment of length 0.3 between the inner and outer radii.
As I said early on this page, most "real-life" problems are "fuzzy" in that we need to make some reasonable assumptions.
Tell us how your students go with it!
8 Jan 2010 at 12:52 pm [Comment permalink]
U r smart zac..very impressive and genuis solution
9 Jan 2010 at 7:29 pm [Comment permalink]
This is an interesting application of radian measure. my only comment is that if the drawing is part of the given information, then the curvature of the arc is already fixed. One is not free to select any radius for the inner or outer curve. Rather, by carefully laying a straight edge against the curve at its two end points, you can estimate its symmetric tangent lines at those two points. Then one can project a matched pair of normal (right angle) lines back into the figure to locate the point "P".
9 Jan 2010 at 8:55 pm [Comment permalink]
Thanks, Doug. I should have mentioned he already knew the inner and outer radius for his window, so he could directly use the formula I gave him. That is, P was determined already by the dimensions he knew.
10 Jan 2010 at 6:28 pm [Comment permalink]
Dear All,
I feel pleasure to interact with you on subject like maths. This is first time I am interacting. I am not a mathematician as such I may be wrong also, but as I am an Engineer, I think I can also add some thing here.
You see, first of all it is important to ask what is the vertical height of the top most point of Arc (Say interior Arc) from horizontal line HI. Say the reader of glass company want this as 0.5 unit, keeping all other dimnesions same as given above. Now if R is the radius of curvature than, we can use the pythogorian equation
R Sqare = (R - 0.5)Square + 2Square
solving this gives R as 4.25.
Once we know R, we can find the angle subtended by Arc, which comes out to be 56.144 degree (0.98 rad), and accordingly the arc length thus can be calculated as 4.1646.
The advantage here is we dont need to know the location of centre of circle.
Normally such arches are preferred with Parabolic shape as it requires to carry load of wall above it. Whatever is the shape whether it is circular, Parabolic, Elliptical or Hyperbolic, we can calculate the length of arc. Your comments please.
thanks,
best regards,
Vinay
30 Mar 2010 at 11:16 pm [Comment permalink]
I would like many, many trigonometry problems with applications to aviation mathematics. I teach trigonometry to a class of professional pilots. They have a lack of interest (understandably) to trig problems that deal with identities, solving trig equation, changing to polar form, etc.
John
3 Apr 2010 at 5:04 pm [Comment permalink]
Hi John
I can certainly understand why your pilots are not very excited about trigonometric identities! I used to "justify" this topic by saying it helps students to better remember the trigonometry ratios (which it certainly does), but there may be more efficient ways to do that.
If I was in your shoes, the first thing I would do is try to change the syllabus topics so they better reflects the students' needs. But that is often not so easy...
I'll keep my eyes out for you and try to include some relevant applications in future IntMath Newsletters.
29 Nov 2011 at 5:24 pm [Comment permalink]
Thanks Murray,
quite interesting. I'm not really certain what Doug meant but I dont think P is fixed. Maybe the x axis is but I do believe varying the y will still give an approximate answer. I'm not good at some fixed equations so I most have to use personally derived eqns that solve for radian and lenght of arc. It's much longer but I tend to remember it more. My answer was 3.53 (had to solve for the circumference which is 30units).
For Vinay, I am really interested in understanding how the pyta's eqn that solved for IM can be used to deduce the arc lenght. I'm also not sure since you got an angle of 4.25 radians when a circle = 6.28 radians ( the diagram does not even seem up to 100 degrees which is about 2 radians).
29 Nov 2011 at 9:54 pm [Comment permalink]
@Paula: Vinay is taking a stab at the location of P, which is fine since it, and the radii, are not fixed necessarily. My diagram is drawn to scale and the angles follow. But if you move P vertically, the central angle will increase.
However, 4.25 is more than 180°, so yes, there is a problem!
8 Jun 2013 at 5:59 pm [Comment permalink]
ok very simple ...and stop using xyz - please
assuming for a moment this is an arc [radius] of a circle
the distance H to I in a straight horizontal line is the chord of the circle ..call it C and we need half of that distance H to P = half C
Chord C = [example 100[
half C = [example 50]
next get a ruler and measure at 90 degrees to C at P up to the inner circle centre of it's arc at H to I - it's called the Sagitta so call it S
S = [example 25]
the sum is simple
Radius = S [squared] + half C [squared]
divided by 2 x S
so Radius = 25 x 25 + 2500 = 3125 divided by 50
= 62.5 which is the radius of the circle
now you can do simple triangle maths to determine the angles which will lead to the arc length in this case 115.91
as you should have ended up with the angle of 106.26 as the central angle of the circle