IntMath Newsletter - Trigonometry tips and a puzzle
By Murray Bourne, 01 Dec 2008
1 Dec 2008
In this Newsletter:
1. Earth Puzzle
2. Math tip - Trigonometry
3. From the math blog
4. Solution
5. Final thought - 3 kinds of people
1. Earth Puzzle
I walk 20 paces North then turn left and walk another 20 paces West. I turn left again and walk a further 20 paces South. I am amazed to find that I'm back in the same place that I started.
Where am I?
[Hint: This puzzle is related to Earth Geometry that we talked about in the last edition. Solution at the end of this Newsletter.]
2. Math tip - Trigonometry
 A reader asks, "what is trigonometry all about?".
A reader asks, "what is trigonometry all about?".
See my reply here: What is trigonometry all about?
3. From the math blog
1) Project Euler
Project Euler has some interesting math questions that require the use of computer algorithms to solve.
2) Unicode characters for Chinese and Japanese numbers
Unicode characters use hexadecimal numbers (base 16) to display characters from languages like Japanese, Chinese, and Greek.
3) Friday Math Movie - Math Rules!
This week's math movie was a finalist in the X-Box Competition at the 2007 New York Television Festival.
4. Solution
The answer to the puzzle above is that I started at the South Pole. I walked 20 paces North, then 20 paces West, then 20 paces South again, arriving back at the South Pole, where I started.
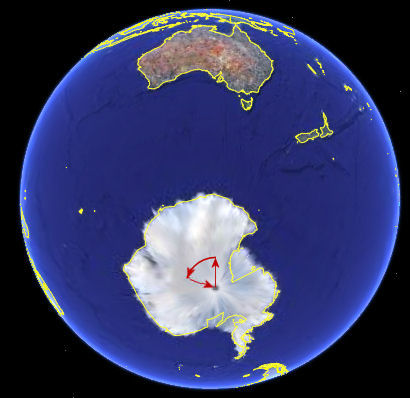
In the picture, it looks like the second and third legs of the journey are not straight. This is one of the intriguing things about Earth Geometry — no lines are straight. (The first leg appears straight because North is straight up on the picture.)
4. Final thought - 3 Kinds of People
There are 3 kinds of people:
1. Not very clever people — the ones who never learn from their mistakes
2. Smart people who do learn from their mistakes
3. Successful people who learn from the mistakes of others
Which kind of person are you?
Until next time.
See the 18 Comments below.
2 Dec 2008 at 1:34 am [Comment permalink]
Good letter.
2 Dec 2008 at 6:32 am [Comment permalink]
In reference to the recent newsletter on Trignometry-the kind of 3 persons. There are 3 persons in 1 sometimes, Mr. Murray. Some persons sometimes will learn, sometimes,they simply don't see it good to work on the mistakes. However, people tend to dwell at a greater percentage of one of the 3 characteristics at times.
It was a challenge to me.
Thanks.
2 Dec 2008 at 12:10 pm [Comment permalink]
Ed: Thanks!
Lani Joe: Yes, it is a challenge. It is sad that people seem to be programmed to repeat mistakes. We don't learn as much as we should...
2 Dec 2008 at 5:23 pm [Comment permalink]
i wonder if you are going to prepare a page a bout derivative. if you do so i will be happy!
thanks for all.
3 Dec 2008 at 7:26 am [Comment permalink]
Very good, especially the last part...I generally find that its harder to get interested in math than actually do it.
Once you start actually enjoying it, you do so much better...
4 Dec 2008 at 1:36 am [Comment permalink]
Kinds of people: binary
There are 10 kinds of people in the world: those who can count in binary and those who cannot. And by the way, never trust a man who can count to 1024 on his fingers!
Kinds of people: ternary
There are only 10 types of people in the world —
those who understand ternary, those who don't, and those who mistake it for binary.
Kinds of people: self-referential paradoxes
There are two kinds of people in the world: those who separate people into two kinds, and those who do not.
There are two kinds of people in this world: those who are good at math, those who are good at English, and those who ain't good at neither.
There are two kinds of people, those who finish what they start and so on...
Dedication to Godel
There are two kinds of people in the world: those who get jokes, and those who don't. Get it?
4 Dec 2008 at 7:54 am [Comment permalink]
rifat: The derivatives topic is on my long list for future IntMath Newsletters. Watch this space!
Josh: Motivation is the key, for sure. As someone once said, “Every accomplishment starts with the decision to try.”
Maria: Thanks for your great list of dichotomies, trichotomies, quadrotomies — and so on... 🙂
4 Dec 2008 at 1:52 pm [Comment permalink]
you are doing good job keep it up
4 Dec 2008 at 3:25 pm [Comment permalink]
[...] Murray Bourne’s IntMath Newsletter this week includes a nice preamble to the study of Trigonometry. I’d like to be able to link to that item specifically when introducing the topic, so maybe I’ll ask him to isolate it if he has the time. [...]
4 Dec 2008 at 9:03 pm [Comment permalink]
Abdul: Thanks for the kind feedback.
Alan: I always have a dilemma - do I put an article like that in a separate post and then send all my subscribers there (which is one extra click of inconvenience and lots of readers will miss it) or do I include it in the body of the Newsletter (where it gets mixed up with the other stuff)?
Update: I've separated it out, at long last Alan. It's now a separate article here:
What is trigonometry all about?
5 Dec 2008 at 5:25 pm [Comment permalink]
I am very happy to see this.
11 Dec 2008 at 9:15 pm [Comment permalink]
HEY GUYS I REALLY LIKE THIS EDITION IT'S REALY INTERESTING PLEASE SEND ME MORE.THANK U
25 Oct 2009 at 12:57 am [Comment permalink]
i must thank the author of this site. this is undoubtedly a great site to learn mathematics. it makes me believe that math is not a fiction, but it takes us into pleasing and imaginary world of ficiton when you are able to unbutton its mystery.
Math has also its mystery, symphony and rythm, but unfortunately most of us fail to discover it. But i must say when you know the way of getting into it then it won't give you anymore pinch. anyway thanks for the tips
28 Jul 2010 at 10:56 pm [Comment permalink]
Hi,
Love the post, but I disagree with your solution to your 'Earth Puzzle':
As the Earth can be approximated to being spherical, the poles are (all but) arbitrary points on a sphere (i.e. the poles, in terms of geometry, have no special significance). This means that your solution should work for /any/ point that I happen to choose on the surface of the Earth. I could, for example, go out into the street outside my house and give it a shot. It wouldn't work.
For the experiment described to be effective, I'd have to walk further. A lot further. To get back to where I started after having made only 3 90 degree left turns (or 3 right ones), each side of the triangle would have to be equal in length to one quarter of the Earth's circumference. This is because the effect of the Earth's curvature becomes more pronounced on larger scales. Or, from the other direction, the smaller the scale you work on, the less pronounced the perceived curvature is (which is why the experiment won't work with only 20 paces- unless you have one hell of an inside leg measurement- anywhere on the Earth).
Your experiment does work, however, if for the second side of the triangle you walk along a line of latitude. This line would be 'straight' in some sense, but not in the plane in which you were walking, so you would have to actually walk a curved path from your own point of view.
The rest of the post is excellent, though, and I'll be bookmarking it for some ideas for the future!
31 Jul 2010 at 11:14 am [Comment permalink]
Hi TeaKayB. Thanks for your response, but indeed, my solution does involve the second side of the triangle being a parallel of latitude. This will happen if you start in 2 places - the North and South Poles (I chose the South Pole for my solution so I could "happen" to include my home country in my diagram 🙂 )
I can see why you want to only include the equator (the point reached when we travel 1/4 of the Earth's circumference) as one of these latitude lines, but in fact, it works for any parallel of latitude.
A key point is what we mean by "turn 90° left". In which plane is that 90 degrees measured? And what makes the Equator any more special for this measurement than the point 20 paces north of the South Pole?
I love spherical geometry!
31 Jul 2010 at 4:07 pm [Comment permalink]
What makes the equator special is that it is the only parallel of latitude on which the conductor of the experiment would be able to walk in, as far as they were concerned, a straight line, as they would be perpendicular to the plane of that parallel's curvature.
Any other parallel would require the walker to consciously /not/ walk in a straight line in order to stay on the line of latitude. This is because anywhere other than the equator, they will not be standing/walking perpendicularly to the line's curvature.
If we are restricting ourself to the 2-dimensional Earth's surface when drawing our triangle, mine (that uses the equator and has sides of length 1/4 of the circumference) is as true a triangle you can get when including three right-angles - each of the three sides are "straight" as far as can be measured in that curved 2D space.
Your 20-pace triangle would not be a triangle on the 2D surface, as additional to being curved in the unseen/ignored 3rd dimension, one of the sides would also be demonstrably curved in the 2 dimensions that we're working in.
Again, it is not the equator itself that is special; it is the size of the shape. The parallels of latitude are arbitrary (in terms of geometry) so if your assertion were true, it would work anywhere on the surface of the Earth. I could /only/ produce what appeared to me to be a 3-right-triangle if the sides were equal in length to 1/4 of the circumference of the sphere on which you're drawing it.
Try it with a marker pen and a ball, or even a balloon- you /cannot/ draw a triangle with three right angles and sides longer or shorter than 1/4 circumference of the ball/balloon without introducing curvature other than the natural curvature of the body that you're drawing it on.
31 Jul 2010 at 5:32 pm [Comment permalink]
OK, it's confession time.
My puzzle question should have read "If you head North for 20 paces, then West for 20 paces, then South for 20 paces, you end up in the same place you started. Where are you?" The issue of 90° and curvature does not arise.
That's what I intended in the first place and I realized my error after your first comment :-), but couldn't resist stirring the pot. Nobody else picked my error!
Thanks for alerting me. I have updated the post.
1 Aug 2010 at 4:46 am [Comment permalink]
Hahaha, yes, I'm a fellow pot-stirrer 😉 That makes much more sense now!
Glad to be of service 😀