Math problem solving and brain activity
By Murray Bourne, 02 Jul 2008
I believe that solving math problems is a very important issue. Mathematics is more than just "doing algebra". If we know how to solve a real-world problems, then we'll have a powerful and important ability, and best of all we'll see why we are doing all this math.
Let's say you have a math problem that is in sentence form. Most people struggle with word problems and one reason is that math word problem solving uses many parts of the brain.
Here are some tips on how to attack math problem solving — and I have included an indication of what goes on in the brain during each step. Here is a diagram of the brain so you can follow along. The front of the brain is on the right of the diagram.
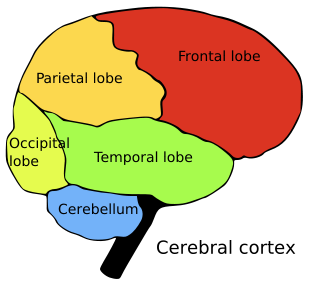
Image source.
a. Read over the whole problem: Understand the whole question first and take special note of the what?, when?, which?, how many? parts of the question, usually at the end.
The areas of the brain that you use for this portion of the math problem are the very back of the brain (your occipital lobe) where you process what you see. You also use the language areas of your brain (a large portion of the left hemisphere, surrounding your left ear).
b. Write down or draw what the question tells you: By listing the information in the question, it helps you to sift through what you already know and it reminds you of the math that might be involved. Once again your left brain is involved in the writing part, in particular Broca's Area and Wernecke's Area, which are above your left ear.
If there is any geometry involved (or graphs, or moving objects, or any other visual element) in the question, draw the situation. For drawing, you use the areas towards the rear top of your brain (the parietal lobes), the area at the top of your head (the sensorimotor region) and the back of your brain (vision).
c. What do they want? Is the quesion asking for a speed, or a time, or a length, or a position, or a cost? Many students answer a word problem by giving an answer that is not what the question actually asked. In the real world, will your boss be impressed if you give a time answer when they actually asked for a cost?
At this point, it is good to estimate the answer and to write down that estimate for checking later. Estimation involves non-language areas of the brain (while exact arithmetic involves language areas).
So far in our math problem solving, we have a good idea what the question has told us and we know what we need to find. We also have an approximation for our answer.
d. Identify the math required: Now you need to make a decision about the math. Will it involve algebra? Or maybe trigonometry? Or logarithms? Maybe it will involve differentiation or perhaps integration? This is where you see the need to actually learn the formulas in each section of math that you study, and not rely 100% on formula sheets. The best way to recognize the math that you need to use, is to know that math in the first place.
This step uses the higher-order thinking areas at the front of the brain (the frontal lobes) and the memory areas of the brain (which tend to be all over).
e. Do the math: Now we need to churn through the algebra (or whatever) to get our answer. Assign variables to the known and unknown quantities in the question. In the brain, this step involves the frontal lobes and the area behind and above the ears.
Your answer must include units (if there are units in the question).
f. Check, check and check: Firstly, check if your answer is close to your estimate. If not, it's back to the drawing board.
Next, read over the question again and check that you have actually found what the question was asking for.
Finally, check all the algebra and arithmetic steps.
Phew! We are done.
Now don't be scared about all the brain activity involved in math problem solving. It's like most human abilities — the more you do it, the easier it becomes and the brain can begin to relax.
George Polya contributed greatly to our understanding of how to solve math word problems. You can see a summary of his approach from his 1957 book "How to Solve It" at G. Polya: How to Solve It.
See the 20 Comments below.
3 Jul 2008 at 4:20 pm [Comment permalink]
its a great article thank u for this full explanation about that programme ,, for me the word questions r not hard ,, i like to solve them ,, but for alot of sudents its a problem ,, what u told us will help in math and also in physics cause every thing in physics talks about the real life
12 Jul 2008 at 10:49 pm [Comment permalink]
its a very very informative and good article which has not only helped me to analyse my ways of doing word problems but will also help me to tell it to the tsudents as a teacher..
15 Jul 2008 at 6:44 pm [Comment permalink]
it's an honour for everything you have done for us. i also guess to know maths means to know how to to explain it' so can i get the better ways of teaching maths. and if ever possible, i would also like you to give us some problems as to train ourselves and try to find our self confidence
20 Jul 2008 at 5:25 pm [Comment permalink]
Thanks for the post, Zac.
Do women process math problems differently to men, or is that just a male chauvinist rumor?
20 Jul 2008 at 11:51 pm [Comment permalink]
i have very much passion about math and physics.
but i can not get any time to practice it coz of my academic studies and economic problem. i like this web very much. i always have the love and respect to the scientists and the person who are working for human being.
22 Jul 2008 at 3:18 pm [Comment permalink]
i like it! when i read this article i have a new ideas know in teaching math in the classroom. thank you so much...
Peace!
22 Jul 2008 at 5:00 pm [Comment permalink]
Steph: It may be true that women have an advantage when it comes to doing math problems. Since women have a larger corpus callosum (the tissue that connects the left and right sides of the brain) than men, they have more pathways between the left and right hemispheres. So all this activity between different parts of the brain is actually less effort for women.
As a man, I'm jealous.
However, this issue of male and female brain differences is disputed. See Characterization of sexual dimorphism in the human corpus callosum (full article) and Sex Differences in the Human Corpus Callosum: Myth or Reality? (abstract only).
31 Jul 2008 at 10:48 am [Comment permalink]
Thankyou verymuch
31 Jul 2008 at 2:18 pm [Comment permalink]
Great article and very helpful.
I always thought girls were not supposed to be able to do math as well as boys. Certainly there are very few girls in higher math and in fields like engineering.
And you're saying they actually have an advantage? Wow.
6 Aug 2008 at 11:41 am [Comment permalink]
It is good. It helped me to solve mathematical problems with more patience.
29 Sep 2008 at 2:57 am [Comment permalink]
I am a math teacher just starting to explore how and where the brain processes math information. This article illustrates that nearly EVERY part of the brain is utilized in a word problem. As a teacher, it is my job to break down a problem so students can comprehend each part, this information is extremely helpful, especially if a student has a specific learning difficulty. I will be able to better scaffold their assignments. Thank you!!
29 Sep 2008 at 1:47 pm [Comment permalink]
Hi Nancy and thanks for your comment.
Good on you for exploring this issue. I wish more math teachers would do so and then rather than turning their students off with mindless "drill and kill", they may be more aware of what actually triggers - and maintains - interest in a math class.
6 Jan 2010 at 5:11 am [Comment permalink]
HI and thnx for this website it is an honour since i flunk math to get to know this it really helps so thnx eyy and i agree with ladies being better in math srry i dont use long words:p
18 Sep 2010 at 10:14 am [Comment permalink]
good article. pls tell me which part of brain to be stimulated (left or right) for solving maths
18 Sep 2010 at 10:18 am [Comment permalink]
Hi S. Mathematical thinking occurs in most parts of the brain. This video may give you some insight: Right brain math.
15 May 2011 at 1:17 am [Comment permalink]
How does this affect students who have disabilities, like severe learning disabilities, intellectual disailbities, etc.? Are there studies to show how their brain functioning can be stimulated or helped to increase their problem solving skills? It appears they are such concrete thinkers that they cannot seem to get to the abstract and stick with the algorithm that is comfortable to them for all problems and don't comprehend past that thought?
15 May 2011 at 8:32 am [Comment permalink]
This affects those with learning difficulties on many levels - attention, higher-order thinking, processing words and numbers, connecting back to earlier parts of the problem, and so on. There has been quite a bit of research on this. This Google search shows up a lot of interesting articles.
12 Feb 2014 at 5:35 am [Comment permalink]
Interesting article. I was curious about the relationship between the area of the brain that does math and my headaches. I have Multiple Sclerosis and every time I do algebra I feel like my head is going to explode. The lesions are in the occipital and parietal lobes. Now I know I am not being a big baby when it comes to algebra.
12 Feb 2014 at 8:45 am [Comment permalink]
Thanks for sharing, Kathleen. All the best with it!
20 Jan 2018 at 3:49 am [Comment permalink]
I like it helps .me.on hard word problems☺☺