Math of the Great Summer Brain Drain
By Murray Bourne, 23 Jul 2010
In an IntMath Newsletter last year, I wrote about the Forgetting Curve.
Philosopher Hermann Ebbinghaus conducted experiments on his own memory, where he memorized a set of 3-letter nonsense syllables and then tested himself at intervals to see how much he could remember. This was the resulting data, showing that after only about 3 days, he forgot 75% of what he learned.
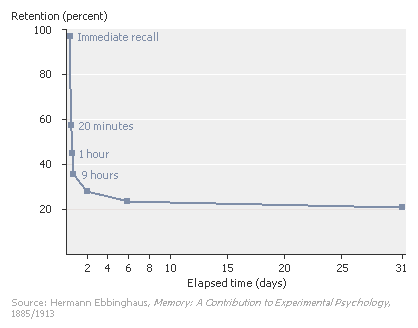
[Source: Encarta (link no longer available)]
Now, this looks quite bleak, but there are some things to consider:
- He was learning nonsense syllables which had no meaning. (Similarly, if you try to learn math formulas without understanding them, it is also easy to forget them.)
- The content he was learning had no emotional significance for him (since it was nonsense), and so it was harder to remember. He had no attachment to what he was learning, except for the sake of his experiment. We remember best the things that have most emotional significance (positive or negative).
Use it or you lose it
The following diagram is labeled "Ebbinghaus Forgetting Curve" but it really has an emphasis on how effective learning works, rather than forgetting.
The idea in this diagram is if we learn something today, we forget most of it quickly (the lower black dotted line, which is an exponential decay curve).
But if we learn the material again (we can remember 100% again), we retain more this time (the second lowest curve). The more we repeat the learning process, the more we retain and the less work we have to do to "top up" so we get back to 100% mastery. This is represented by the orange dips and spikes, following the shape of the increasing green curve.

Image source: Phase-6 (no longer available)
Notice also that we can space out the repetitions as time goes on, but the most important ones are at the beginning (within 24 hours is crucial).
Of course, this is what homework is all about. If you practice at night what you learned in school during the day, it will be retained much better. Too many students leave homework to the last minute, and have forgotten all the theory behind it already, so find it difficult.
An expert is someone who has not only repeated things over and over, but has also explored it from many different angles, worked with it, solved problems with it and then really knows the material extremely well.
Just before we leave this diagram, it's interesting to note the forgetting curve has an exponential decay shape, while the memory curve (the green one) is logarithm-shaped (which is the inverse function for the exponential curve). See more on exponential and logarithm curves.
What happens during summer?
Sadly, most students totally avoid books during summer, and so forget much of what they learned during the previous semester. What a waste!
Just spending 30 minutes a day on math (or science, or reading, or whatever) during summer makes a huge difference when school starts again.
What are your summer learning goals?
It's not quite that simple
Of course, effective memory is much more involved than simple repetition. If we don't understand what we're doing, it still won't "stick". But once you do understand it, and know how to use it, one of the best ways to retain it is through repetition.
One way to make memorizing more efficient is to associate the concept (or formula, or word) with an image or an action. There are many resources on this.
Work smart, not hard
It's always a struggle when school starts again after a long break because much has been forgotten. It's much easier if your learning is kept "on the boil" during summer.
Feel free to use the resources at IntMath.com to help you keep your math "on the boil"!
See the 4 Comments below.
23 Jul 2010 at 1:31 pm [Comment permalink]
Dear Murray Bourne
After a long gap I m writting to you abt d interesting maths subject. Actually though I m in touch with evry topics but due to busy schedule, I could not comment on yr page. Hoipe u will continue with good topics
With regards,
suprakash chakraborty
23 Jul 2010 at 11:30 pm [Comment permalink]
The one who masters it most is he who repeats it frequently. Retention co-exists with repetition.
3 Aug 2010 at 7:42 pm [Comment permalink]
Just happens that the "use it or lose it" coincides with Jay Giedd's idea when it comes to teenage brains.
The PBS programme is here.
And the Nature article by Kendall Powell which I read earlier was a little harder to find.
Jacqueline
26 Aug 2010 at 2:14 pm [Comment permalink]
Though i am newly subscribed to this site, having been a mathematics student in the university for three years now, i must say its quite interesting to read the posts here. Iam very gratefull, cheers.