Taxicab Geometry
By Murray Bourne, 09 Aug 2010
Many cities are built on a grid pattern where city blocks are approximately square. The grey dotted lines in the following diagrams represent streets.
A taxi driver needs to go from point C to B. She decides to take the following route (depending on her local knowledge of traffic and one way streets and so on), where she heads north along CD, turns East for DF, then North again, and so on until she reaches B.
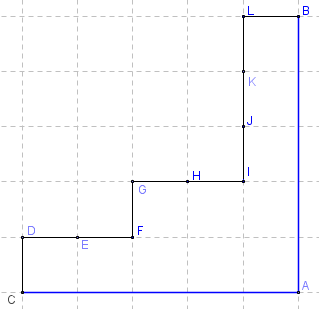
Or she could have more simply travelled from C to A, then A to B. If CA = AB = 1 km, then the total journey is 2 km, no matter which route she took. (Distance CD = 200 m and there are 10 such blocks, so 2 km is the total distance.)
This gives rise to an interesting type of geometry called Taxicab Geometry, first proposed by Hermann Minkowski in the 19th century.
How Many Routes?
There are clearly many different ways of going from C to B. If we assume she is an honest taxi driver (and doesn't go away from B at any time), then she can only travel North or East.
Let's consider her first decision. She can only go North or East, so 2 choices:
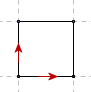
Now, looking at the first 4 city blocks, we see there are 6 choices:
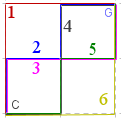
Continuing, we find the following number of possible routes as we add more rows and columns of city blocks:
2 (for 1×1), 6 (for 2×2), 20 (for 3×3), 70 (for 4×4), ...
You may recognise these as being the middle number of each second row in Pascal's Triangle.
This is also connected with counting theory and we can show that for our 10×10 grid, our taxi driver will have
20C10 = 184,756 choices for getting from C to B.
An interesting question arises
Let's now take a route that gives us a more diagonal shape, as follows.
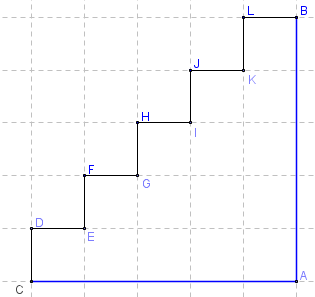
Once again, our total distance is going to be 2 km.
But for interest, let's imagine we can actually travel along lanes that pass in the middle of the city blocks as follows.
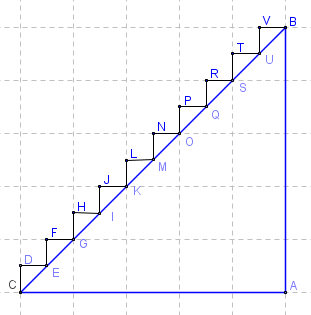
Our total distance is still 2 km.
But now let's push it even more, and take many tiny zig-zags as follows. Our total distance is still 2 km.
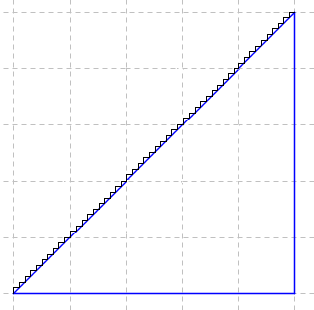
But what is the limit of this process? Won't we actually be smoothly travelling up the diagonal, since we can't even steer the car North then East, since the steps are too small?
And now we have the interesting question. What will be the distance the taxi travels up this smooth diagonal?
Well, √2, of course, from Pythagoras' Theorem. So the distance from C to B is no longer 2 km, but around 1.414 km, or 0.586 km less than 2 km!
Where did that 0.586 km go?
See the 20 Comments below.

10 Aug 2010 at 9:49 am [Comment permalink]
The limit of the lengths is √2 km, but the length of the limit is 2 km. The reason that these are not the same is that length is not a continuous function. Very small perturbations in a curve can produce large changes in the length.
This is related to the coastline paradox, which is a motivating example in fractal geometry.
13 Aug 2010 at 11:14 am [Comment permalink]
The taxi cab geometry is very simple but very interesting. The students can also interpret this way, as we climb a up the stairs ,flight of steps we cover a minimum distance of the length of the floor below the stairs and the height of the wall. In the diagram given above floor length is CA and height of the wall is AB.Is the word minimum distance appropriate?
18 Aug 2010 at 3:25 am [Comment permalink]
I have a question of you have a grid which is 10x 10 but there is a blanc space in the middle of 2x2. how can you find out how many ways there are to get from A to B?
18 Aug 2010 at 8:59 pm [Comment permalink]
Hi Stephanie. The blank space is a city block, so you need to go around it!
19 Aug 2010 at 1:24 am [Comment permalink]
I propose this explanation:
The two trajectories (one diagonal and the other composed of the north-east zigzag) are effectively the same route. It is acknowledged that 0.9999...=1 since one cannot say there is a difference (you cannot say there is always a difference however negligable because the very idea of limit is that it infintely approaches the target- see relating article on this). Here, I believe, we can confidently assent to a congruence of situation. One zigzag can be so small that its total length (north+east) would be 1/n+1/n as n approaches infinity. 2/infinity=0. The same may be said of the hypotenuse that can be constructed on this zigzag, its length would be sqrt(2)/infinity equalling zero.
To work out the difference of all zigzags and all hypotenuses, we have to times their indivdual lengths by infinity ( Both can be calulated by 0*infinity)
The difference of 0.586km is the direct result of such mishandling of infinity and its pairing to yet another curious number 0.
0*infinity does not follow laws of ordinary numbers, for anything divided by zero is infinity (or zero times infinity is anything). This absurdity can be demonstrated by the case where 2 can be shown to equal 1 if division by zero is acceptable. It is not. Nor is 0 times infinity.
I admit this explanation is challengeable to questions I cannot answer, in particular how the 2 and the sqrt(2) came about anyway seeing I have used the term 'anything' for the resulting sums.
And if you have read this far, I applaud your zeal or rather, critical eye.
19 Aug 2010 at 9:11 am [Comment permalink]
Hi Daochen. Indeed, there are "challengeable" assumptions in what you say (especially the multiplying and diving by infinity parts), but it is an interesting analysis!
23 Aug 2010 at 1:32 pm [Comment permalink]
This is my analysis:
If you approach the limit, although the car moves in a straight line, you have to keep steering the wheel at an infinitely high rate, which makes the car seem slower. Since you are actually traveling at same velocity compared with the normal zigzag method(let's assume that), you have to travel more distance that what you seem. That distance you have to travel more is the 0.586m.
24 Aug 2010 at 2:01 pm [Comment permalink]
Practical concern:
The 0.586 km would be such a waste. If only those city blocks had a hole through them.
26 Aug 2010 at 9:06 pm [Comment permalink]
I found an interesting discussion on this post over at reddit.
5 Nov 2010 at 2:46 am [Comment permalink]
This is a well known old dialectical problem; however written in interesting way. You are making relation between the continuous and discrete space, which is wrong. You can find many similarities with the Zenon's appories (paradoxes) - "Achilles and the turtle", "stadium", "the arrow" and "dichotomy". The problem is clearly philosophical and the physical solution comes with the quantum mechanics.
Cheers
5 Nov 2010 at 4:07 am [Comment permalink]
Let me summarize what I said above with a cite from V.I.Lenin:
- The movement is the essence of the time and space. Two primary notions describe this essence: the continuity and the discreteness. The movement is a unity between the continuesness of the time and space and the discreteness of the time and space. Therefore the movement is contradiction, a unity of contradictions...
The same applies (on my opinion) for all other spaces. The dimensions of the spaces are properties of the matter, so we cannot say "the matter is IN the space". There is dimensional continuum. Therefore you should not mix discrete with continuous.
26 Nov 2010 at 1:17 am [Comment permalink]
The number of paths the honest taxi driver can take is incorrect. Since she is honest and can only go either North or East at any one time,each of her possible paths will consist of 10 line segments (blocks). There will be 5 North and 5 East. Once she has decided which blocks will be North (or East), the entire route is determined.Thus the total number of possible paths is
10C5 = 252
24 Dec 2010 at 11:18 am [Comment permalink]
where i can found the definition and theorems taxicab geometry?
24 Dec 2010 at 4:25 pm [Comment permalink]
Hi Kurnia. This search result could be a good place to start!
15 Jan 2011 at 7:52 pm [Comment permalink]
I've tried to find there ... but I still can not find the theorems...btw its okay...thank u...
29 Jan 2011 at 1:11 pm [Comment permalink]
The "missing" amount simply shows that the definition of arclength depends explicitly on one's choice of metric. Theorems which have been proven in (R^2,Euclid. metric) are not valid in (R^2,Taxicab metric) because they are different metric spaces. Since it is a finite dimensional space, the metrics are equivalent though, so a curve is rectifiable with respect to the Euclid. metric if and only if it is rectifiable with respect to the taxicab metric. Sorry if that is too technical.
22 Jun 2012 at 8:35 am [Comment permalink]
How will the formula change for a rectangular grid?
9 Mar 2017 at 3:49 pm [Comment permalink]
[…] a taxi would travel in a grid plan. The fifteenth Euler problem asks to determine the number of possible routes a taxi can take in a city of a certain […]
10 Aug 2017 at 5:13 pm [Comment permalink]
[…] Задачата е взета от блога SquareCirclez. […]
8 Jul 2018 at 5:06 am [Comment permalink]
[…] a taxi would travel in a grid plan. The fifteenth Euler problem asks to determine the number of possible routes a taxi can take in a city of a certain […]