Skip to main content
Interactive Mathematics
Search IntMath
Close

Math of drugs and bodies (pharmacokinetics)

By Murray Bourne, 01 Feb 2010

Pharmacokinetics is the process whereby substances (like food and drugs) are ingested into the body (via mouth or needles) and processed. We'll concentrate on drugs.

syringe
Preparing a syringe.

The process of pharmacokinetics has 5 steps:

  • Liberation - the drug is released from the formulation.
  • Absorption - the drug enters the body.
  • Distribution - the drug disperses throughout the body
  • Metabolism - the drug is broken down by the body.
  • Excretion - the drug is eliminated from the body.

Of course, each drug needs to act on the body in a different way. Some drugs need to be absorbed quickly (like nitroglycerin if we are having a heart attack) and preferably eliminated quickly (otherwise toxins build up in the blood). For other drugs, we want slow absorption so we get maximum benefit and don't lose a lot of it from excretion.

So when your doctor prescribes (say) "take 2 tablets 3 times a day after food", this is based on the desirable levels of drug concentration and known levels of distribution, metabolism and excretion in the body.

What's the math?

When the nurse first administers the drug, the concentration of the drug in the blood stream is zero. As the drug moves around the body and is metabolized, the concentration of the drug increases.

There comes a point when the concentration no longer increases and begins to decline. This is the period when the drug is fully distributed and metabolism is taking place. As time goes on, the drug concentration gets less and less and falls below a certain effective amount. Time to take some more pills.

We can model such a situation mathematically with a differential equation. It has 2 parts - an absorption part and an elimination part. At first, absorption (increasing drug concentration) takes precedence and over time, elimination (decreasing concentration) is the most important element.

We have the following variables:

D = drug dose given

V = volume distributed in the body

C = concentration of the drug at time t

F = fraction of dose which has been absorbed (also called bioavailability)

A = absorption rate constant

E = elimination rate constant

t = time

Absorption part: This depends on the amount of the drug given, the fraction that has been absorbed and the absorption rate constant. It decreases as time goes on. The expression for absorption is given by:

A × F × D × e-At

Elimination part: The elimination dynamic is affected by the elimination constant, the volume distributed in the body and the concentration left of the drug. The expression for this part is:

E × V × C

For our model, we need to subtract the elimination part from the absorption part (since the absorption part increases the concentration of drug and the elimination part decreases it). Our differential equation is as follows:

DE-0

We now substitute some typical values for our variables (without units to keep things simple. Note C is a variable (not a constant here), the one for which we seek an expression in t.)

DE-1

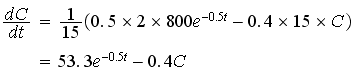
Solving this differential equation (using a computer algebra system), gives the concentration at time t as:

C(t) = 533.3(e−0.4t − e−0.5t)

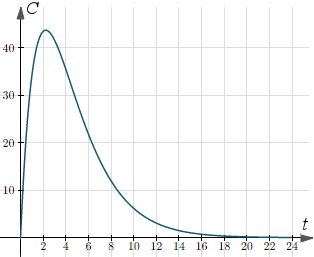
pharmacokinetics

We can see in the graph the portion where the concentration increases (up to around t = 2) and levels off. The concentration then decreases to almost zero at t = 24.

Pharmacokinetics is yet another interesting "real life" application of math.

[Based on: A First Course in Pharmacokinetics.
Photo credit: Syringe]

See the 34 Comments below.

Related posts:

  1. The melting Arctic - a disturbing application of math Here's a few simple mathematical models that describe the growth of ice and how it...
  2. Math of mobile and cordless phones Are DECT phones safe? What is the mathematics behind the decision?...
  3. Math movie: The surprising math of cities and corporations This video discusses some of the reasons - and solutions - for global warming. It's...
  4. Movie: What doctors don’t know about the drugs they prescribe Ben Goldacre exposes a dirty truth the drug companies don't want you to know...
  5. Intmath Newsletter - Graphs, pharmacokinetics, color blindness In this Newsletter 1. Math tip (a) – Graphs using free math software 2....

Posted in Mathematics category - 01 Feb 2010 [Permalink]

34 Comments on “Math of drugs and bodies (pharmacokinetics)”

  1. rashmi says:
    2 Feb 2010 at 11:16 am [Comment permalink]

    hey its nice ..i wondered y ppl distinguish between math and bio now reading this i can say its all abt science ...
    any thing comes from any subject..:)

  2. SueD says:
    3 Feb 2010 at 8:21 am [Comment permalink]

    Fantastic ... always looking for great examples and this is explain rather nicely .. thanks for passing this on!

  3. Shadreck Mpanga says:
    3 Feb 2010 at 10:38 pm [Comment permalink]

    Wow! I now understand cleary why overdose of certain drugs can kill a human being.Please continue saving Human lives with such information.

  4. Munzir says:
    6 Feb 2010 at 4:56 am [Comment permalink]

    I see, so that's how the doctors knows how to distribute the drugs to the patients. Thanks for the research, it really broadens up one's mind in terms of how maths apply to daily life

  5. Aiza says:
    21 Feb 2010 at 5:21 pm [Comment permalink]

    nice...very informative....thanks for the information

  6. Ike says:
    28 Dec 2010 at 12:56 pm [Comment permalink]

    Great. A typical example of using math to explain how things work.

  7. Peter says:
    21 Sep 2015 at 5:57 am [Comment permalink]

    max occurs around t = 2.23, not 3

  8. Murray says:
    22 Sep 2015 at 11:07 am [Comment permalink]

    @Peter: Thanks for your feedback. It is qualified by the word "around" and is descriptive, not intended to provide any particular accuracy.

    But agreed, it's closer to 2 than 3, so I modified the post.

  9. Rafael says:
    15 Dec 2015 at 11:19 am [Comment permalink]

    Why is the differential equation divided by the volume?

  10. Murray says:
    15 Dec 2015 at 12:11 pm [Comment permalink]

    @Rafael: In general, the concentration (C) of any substance is the amount (A) of that substance per unit volume (V).

    An eye drop of food coloring in a thimble of wine has a much higher concentration than the same eye drop of food coloring placed into a swimming pool.

  11. Rafael says:
    16 Dec 2015 at 1:26 pm [Comment permalink]

    How would you solve this differential equation without using a computer algebra system?

  12. Murray says:
    16 Dec 2015 at 2:59 pm [Comment permalink]

    @Rafael: This is a first order linear ODE. See: Linear DEs Order 1

    Instead of x and y, "t" is the independent variable, and "C" is dependent.

    \frac{{d}{C}}{{{\left.{d}{t}\right.}}}+{0.4}{C}={53.3}{e}^{-{0.5}{t}}

    The integrating factor is

    \text{IF}={e}^{{\int{0.4}{\left.{d}{t}\right.}}}={e}^{{0.4}{t}}

    So the solution to the DE is:

    {C}{e}^{{0.4}{t}}=\int{\left({53.3}{e}^{-{0.5}{t}}{e}^{{0.4}{t}}\right)}{\left.{d}{t}\right.}+{K}

    =\int{53.3}{e}^{-{0.1}{t}}{\left.{d}{t}\right.}+{K}

    =-{533}{e}^{-{0.1}{t}}+{K}

    At {t}={0} the are no drugs in the patient's body, so {C}={0}.

    Substituting:

    {\left({0}\right)}{C}{e}^{{{0.4}{\left({0}\right)}}}=-{533}{e}^{{-{0.1}{\left({0}\right)}}}+{K}

    {0}=-{533}+{K}

    So

    {K}={533}

    Then

    {C}{e}^{{0.4}{t}}=-{533}{e}^{-{0.1}{t}}+{533}

    Dividing through by {e}^{{0.4}{t}} and tidying up gives:

    {C}={533}{\left({e}^{-{0.4}{t}}-{e}^{-{0.5}{t}}\right)}

    I hope it helps.

  13. Rafael says:
    17 Dec 2015 at 9:29 am [Comment permalink]

    How did you get from 53.3 to 533?I understand you divided that side of the equation by e^0.4 but how is the coefficient 53.3 affected?

  14. Rafael says:
    17 Dec 2015 at 9:46 am [Comment permalink]

    And why is e^0.4 still on the left side if you divided e^0.4 on both sides? Thank you.

  15. Murray says:
    17 Dec 2015 at 10:21 am [Comment permalink]

    @Rafael: I noticed I had a typo in this line

    =\int{533}{e}^{-{0.1}{t}}{\left.{d}{t}\right.}+{K}

    It should have been this (I've amended the post):

    =\int{53.3}{e}^{-{0.1}{t}}{\left.{d}{t}\right.}+{K}

    The {53.3} becomes -{533} because

    =\int{e}^{-{0.1}{t}}{\left.{d}{t}\right.}=\frac{{e}^{-{0.1}{t}}}{-{0.1}}+{K}=-{10}{e}^{-{0.1}{t}}+{K}

    For the last part,

    {C}{e}^{{0.4}{t}}=-{533}{e}^{-{0.1}{t}}+{533}

    Divide through by {e}^{{0.4}{t}}

    {C}=-{533}{e}^{-{0.5}{t}}+{533}{e}^{-{0.4}{t}}

    Factor and rearrange:

    {C}={533}{\left({e}^{-{0.4}{t}}-{e}^{-{0.5}{t}}\right)}

  16. Jenn says:
    24 May 2016 at 8:19 am [Comment permalink]

    What are the units for the concentration at the end? I know it must be something per L or mL...

  17. Murray says:
    25 May 2016 at 8:29 pm [Comment permalink]

    Jenn

    Typical units for this problem would be:

    D (mL)

    V (mL)

    C (mL / kg) (of body mass)

    F (unitless)

    A (mL / h)

    E (mL / h)

    t (h)

    So the units for C at the end of the problem would be mL / kg.

  18. William Taul says:
    15 Dec 2016 at 10:20 pm [Comment permalink]

    How can F=2? If you have a drug that is 100% effective, then the bioavailability=F=1, which shold be the maximum.

  19. Murray says:
    18 Dec 2016 at 11:09 am [Comment permalink]

    @William: I can't find anywhere in my article or in anyone's comments where it has F=2, so I don't quite get your point.

  20. FOD Fireball's Observations of the Day February 7 and 8, 2017 - fireballnotes.com says:
    9 Feb 2017 at 3:47 pm [Comment permalink]

    […] before calculators came along), exponential growth (of populations, money (compound interest) or drug concentrations over time) and complex numbers (which were used to design the computer or mobile device you are reading this […]

  21. Allie says:
    27 Apr 2017 at 7:18 am [Comment permalink]

    What does 'volume distributed in the body' mean? The volume of the drug in the body, the volume of the body itself?

    Also, could units for drug dosage be change to grams if absorption constant and elimination constant were also changed to grams/hour?

  22. Murray says:
    27 Apr 2017 at 3:35 pm [Comment permalink]

    @Allie: I think this will answer your first question: https://en.wikipedia.org/wiki/Volume_of_distribution

    Yes, you would be able to change units like this (as long as everything balances out - if it's g/h on the left, it needs to be g/h on the right.)

  23. Bucho Morton says:
    9 Oct 2017 at 4:22 am [Comment permalink]

    You have an error in comment 12, where you found your integrating factor. You included 0.4t in the integral - however, that shouldn't have shown up until the integral, itself. And then again, when you presented the solution to the DE, you included t as a multiple of the constant, rather than a multiple of the exponent.

  24. zac says:
    9 Oct 2017 at 4:45 pm [Comment permalink]

    @Bucho: Thanks for pointing out the typos. I've amended them now. (You may need to refresh the page to see the update.)

  25. Bucho says:
    10 Oct 2017 at 4:36 am [Comment permalink]

    No problem. Thanks for doing a good work. Not many people have the ambition, and even fewer have the ability. 😉

  26. Julia says:
    17 Oct 2017 at 10:57 am [Comment permalink]

    How did you create this graph? Where did you get the x and y values for the graph?

  27. zac says:
    17 Oct 2017 at 7:24 pm [Comment permalink]

    @Julia: As it says in the article, I used a computer algebra system to solve the differential equation. You can get Wolfram|Alpha to do it for you (for free), like this:

    W|A solution

  28. FOD Fireball's Observations of the Day February 1st through 7th 2018 - fireballnotes.com says:
    8 Feb 2018 at 1:59 pm [Comment permalink]

    […] for hundreds of years before calculators came along), exponential growth (of populations, money or drug concentrations over time) and complex numbers (which were used to design the computer or mobile device you are reading this […]

  29. Bob Huffman says:
    30 Jun 2018 at 12:03 am [Comment permalink]

    1. If one wanted to apply this to a real life situation where would one find the needed constants? For example, hydrocodone?
    2. If one were addicted to hydrocodone and the Dr says to withdraw slowly could this kind of calculation be used to show the recovering addict exactly what the concentration of the drug is at any given time, and predict what it will be in the future, so he can administer the drug accurately, with the goal being to slowly reduce the highest concentrations while making sure it doesn't go too low too fast, which might lead to relapse?

    3. Has this approach to drug withdrawal been used before?

  30. FOD Fireball's Observations of the Day February 4th through 7th 2020 - fireballnotes.com says:
    7 Feb 2020 at 7:27 am [Comment permalink]

    […] for hundreds of years before calculators came along), exponential growth (of populations, money or drug concentrations over time) and complex numbers (which were used to design the computer or mobile device you are reading this […]

  31. Yarne Dufoer says:
    22 Feb 2023 at 3:49 am [Comment permalink]

    Hello,
    How is it possible that F = 2? Isn't 1 the maximum for this number? The biomedical availability can't be 200% right?

  32. Yarne Dufoer says:
    22 Feb 2023 at 4:51 am [Comment permalink]

    Hello,
    What is the difference between the dose give (D) and the volume (V)?

  33. Yarne Dufoer says:
    8 Mar 2023 at 12:19 am [Comment permalink]

    I see in your calculations that you have used 2 for bioavailability. Isn't the maximum bioavailability 1 (100%)?

  34. Dufoer Yarne says:
    9 May 2023 at 4:37 pm [Comment permalink]

    Hello

    I saw in your article that you are using 2 as your value for the bioavailibility. I don't understand how this value can be more than 1 as the maximum bioavailibility is 100%, which equals to 1.
    Could you further explain your choice of using 2?

    Thank you for your response
    Dufoer Yarne

Leave a comment




Comment Preview

HTML: You can use simple tags like <b>, <a href="...">, etc.

To enter math, you can can either:

  1. Use simple calculator-like input in the following format (surround your math in backticks, or qq on tablet or phone):
    `a^2 = sqrt(b^2 + c^2)`
    (See more on ASCIIMath syntax); or
  2. Use simple LaTeX in the following format. Surround your math with \( and \).
    \( \int g dx = \sqrt{\frac{a}{b}} \)
    (This is standard simple LaTeX.)

NOTE: You can mix both types of math entry in your comment.

top

Tips, tricks, lessons, and tutoring to help reduce test anxiety and move to the top of the class.