6. The Hyperbola

Cooling towers for a nuclear power plant have a hyperbolic cross-section.
[Image source: Flickr.]
A hyperbola is a pair of symmetrical open curves. It is what we get when we slice a pair of vertical joined cones with a vertical plane.
How do we create a hyperbola?
Take 2 fixed points A and B and let them be 4a units apart. Now, take half of that distance (i.e. 2a units).
Now, move along a curve such that from any point on the curve,
(distance to A) − (distance to B) `= 2a` units.
The curve that results is called a hyperbola. There are two parts to the curve.
Let's see how this works with some examples.
On this page...
More Forms of the Equation of a Hyperbola
Even More Forms of the Equation of a Hyperbola
Applications of Hyperbolas
- Navigation: Ship's navigators can plot their position by comparing GPS signals from different satellites. The technique involves hyperbolas.
- Physics: The movement of objects in space and of subatomic particles trace out hyperbolas in certain situations.
- Sundials: Historically, sundials made use of hyperbolas. Place a stick in the ground and trace out the path made by the shadow of the tip, and you'll get a hyperbola.
- Construction: Nuclear power plant smoke stacks have a hyperbolic cross section as illustrated above. Such 3-dimensional objects are called hyperboloids.
Example 1
Let the distance between our points A and B be 4 cm. For convenience in our first example, let's place our fixed points A and B on the number line at (0, 2) and (0, −2), so they are 4 units apart. In this case, a = 1 cm and 2a = 2 cm.
Now we start tracing out a curve such that P is a point on the curve, and:
distance PB − distance PA `= 2` cm.
We start at `(0, 1)`.
Shown below is one of the points P, such that `PB − PA = 2`.
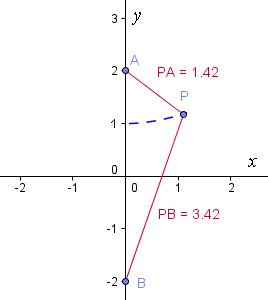
If we continue, we obtain the blue curve:
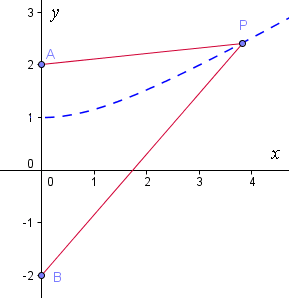
Now, continuing our curve on the left side of the axis gives us the following:
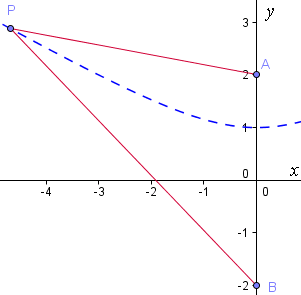
We also have another part of the hyperbola on the opposite side of the x-axis, this time using:
distance PA − distance PB = 2.
Once again a typical point P is shown, and we can see from the lengths given that `PA − PB = 2`.
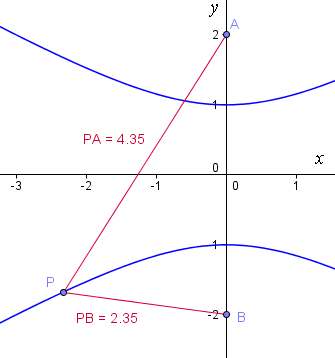
We observe that the curves become almost straight near the extremities. In fact, the lines `y=x/sqrt3` and `y=-x/sqrt3` (the red dotted lines below) are asymptotes:
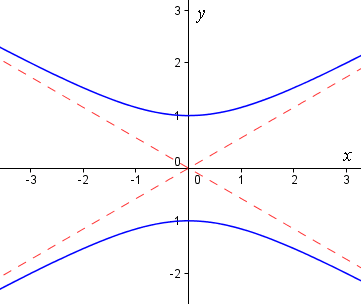
[An asymptote is a line that forms a "barrier" to a curve. The curve gets closer and closer to an asymptote, but does not touch it.]
In Example 1, the points `(0, 1)` and `(0, -1)` are called the vertices of the hyperbola, while the points `(0, 2)` and `(0, -2)` are the foci (or focuses) of the hyperbola.
The equation of our hyperbola
For the hyperbola with a = 1 that we graphed above in Example 1, the equation is given by:
`y^2-x^2/3=1`
Notice that it is not a function, since for each x-value, there are two y-values.
We call this example a "north-south" opening hyperbola.
Where did this hyperbola equation come from?
The equation follows from the distance formula and the requirement (in this example) that distance PB − distance PA = 2.
Here's the proof.
Proof
For any point P(x, y) on the hyperbola,
`text(distance)\ PB=sqrt(x^2+(y+2)^2`
`text(distance)\ PA=sqrt(x^2+(y-2)^2`
Since PB − PA = 2 in our example, then:
`sqrt(x^2+(y+2)^2)-sqrt(x^2+(y-2))=2`
Rearrange:
`sqrt(x^2+(y+2)^2)=sqrt(x^2+(y-2))+2`
Square both sides:
`x^2+(y+2)^2` `=[x^2+(y-2)^2]` `+4sqrt(x^2+(y-2)^2)+4`
Expand brackets and simplify:
`2y-1=sqrt(x^2+(y-2)^2`
Square both sides again:
4y2 − 4y + 1 = x2 + y2 − 4y + 4
Simplifying gives the equation of our hyperbola:
`y^2-x^2/3=1`
The asymptotes (the red dotted boundary lines for the curve) are obtained by setting the above equation equal to `0`, rather than `1`.
`y^2-x^2/3=0`
This gives us the 2 lines:
`y=-x/sqrt3`, and `y=x/sqrt3`
Interactive graph
See an interactive graph of this example, and the others on this page, here:
General Equation of North-South Hyperbola
For the hyperbola with focal distance 4a (distance between the 2 foci), and passing through the y-axis at (0, c) and (0, −c), we define
b2 = c2 − a2
Applying the distance formula for the general case, in a similar fashion to the above example, we obtain the general form for a north-south hyperbola:
`y^2/a^2-x^2/b^2=1`
Example 2
Here's another example of a "north-south" hyperbola.
It's equation is:
y2 − x2 = 1
"North-South" hyperbola (in green) with its asymptotes (in magenta color).
Similar to Example 1, this hyperbola passes through `1` and `−1` on the y-axis, but it has a different equation and a slightly different shape (and different asymptotes). Where are the 2 foci for this hyperbola? We need to find the value of c.
By inspection (of the equation of this hyperbola), we can see a = 1 and b = 1. Using the formula given above, we have:
b2 = c2 − a2
So
12 = c2 − 12
c2 = 2
c = ±√2
So the points A and B (the foci) for this hyperbola are at A (0, √2) and B (0, −√2).
East-West Opening Hyperbola
By reversing the x- and y-variables in our second example above, we obtain the following equation.
Example 3
x2 − y2 = 1
This gives us an "East-West" opening hyperbola, as follows. Our curve passes through `-1` and `1` on the x-axis and once again, the asymptotes are the lines y = x and y = −x.
"East-West" hyperbola (in green) with its asymptotes (in magenta color).
The general formula for an East-West hyperbola is given by:
`x^2/a^2-y^2/b^2=1`
Note the `x` and `y` are reversed, compared the formula for the North-South hyperbola.
Don't miss the interactive graph of this example, and the others on this page, here:
Technical Definition of a Hyperbola
A hyperbola is the locus of points where the difference in the distance to two fixed foci is constant.
This technical definition is one way of describing what we were doing in Example 1, above.
Hyperbolas in Nature
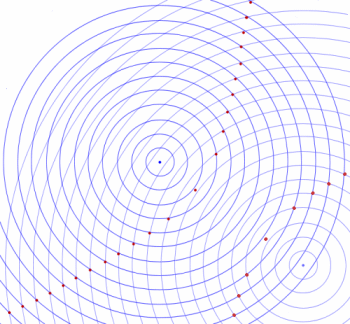
Throw 2 stones in a pond. The resulting concentric ripples meet in a hyperbola shape.
More Forms of the Equation of a Hyperbola
There are a few different formulas for a hyperbola.
Considering the hyperbola with centre `(0, 0)`, the equation is either:
1. For a north-south opening hyperbola:
`y^2/a^2-x^2/b^2=1`
The slopes of the asymptotes are given by:
`+-a/b`
2. For an east-west opening hyperbola:
`x^2/a^2-y^2/b^2=1`
The slopes of the asymptotes are given by:
`+-b/a`
In Examples 2 & 3 given above, both a and b were equal to `1`, so the slopes of the asymptotes were simply ` ± 1` and our asymptotes were the lines y = x and y = −x.
What effect does it have if we change a and b?
Example 4
Sketch the hyperbola
`y^2/25-x^2/4=1`
Answer
First, we recognise that it is a north-south opening hyperbola, with a = 5 and b = 2 . It will look similar to Example 1 above, which was also a north-south opening hyperbola.
We need to find:
- The y-intercepts (there are no x-intercepts for this example)
- The asymptotes
y-intercepts: Simply let x = 0 in the equation given in the question:
`y^2/25-x^2/4=1`
We have:
`y^2/25=1`
Solving gives us 2 values (as expected):
y = -5 and y = 5
Alternatively, we note that the vertices of the hyperbola are a units from the centre of the hyperbola. In this example, it means our vertices will be at `x = 0` and y = -5 and y = 5.
Aymptotes: We have a north-south opening hyperbola, so the slopes of the asymptotes will be given by
`+-a/b`
In this example, a = 5 and b = 2. So the slopes of the asymptotes will be simply:
`-5/2` and `5/2`.
The equations for the asymptotes, since they pass through `(0, 0)`, are given by:
`y = -(5x)/2` and `y = (5x)/2`
So we are ready to include the above information on our graph:
Asymptotes and `y`-intercepts (& vertices in this case).
All that remains is to complete the arms of the hyperbola, making sure that they get closer and closer to the asymptotes, as follows:
"North-South" hyperbola (in green) with its asymptotes (in magenta color).
Interactive graph
See an interactive graph of this example, and the others on this page, here:
Even More Forms of the Equation of a Hyperbola
(1) Possibly the simplest equation of a hyperbola is given in the following example.
Example 5 - Equilateral Hyperbola
xy = 1
This is known as the equilateral or rectangular hyperbola.
Rectangular hyperbola. Asymptotes are the `x`- and `y`-axes.
Notice that this hyperbola is a "north-east, south-west" opening hyperbola. Compared to the other hyperbolas we have seen so far, the axes of the hyperbola have been rotated by 45°. Also, the asymptotes are the x- and y-axes.
Hyperbola with axis not at the Origin
(2) Our hyperbola may not be centred on (0, 0). In this case, we use the following formulas:
For a "north-south" opening hyperbola with centre (h, k), we have:
`((y-k)^2)/a^2-((x-h)^2)/b^2=1`
For an "east-west" opening hyperbola with centre (h, k), we have:
`((x-h)^2)/a^2-((y-k)^2)/b^2=1`
Example 6 - Hyperbola with Axes Shifted
Sketch the hyperbola
`((x-2)^2)/36-((y+3)^2)/64=1`
Answer
We note that this is an "east-west opening" hyperbola, with a = 6 and b = 8.
The center of this hyperbola will be at (2, -3), since h = 2 and k = -3 in this example.
The best approach is to ignore the shifting (for now) and figure out the other parameters for the hyperbola.
So I'm assuming (for this part) that the hyperbola is actually `X^2/36+Y^2/64=1`, and I'll use upper case X and Y.
The vertices of the parabola are found when Y = 0. This gives us X = -6 or X = 6.
The asymptotes will have slope `-8/6 = -4/3`, OR `8/6 = 4/3`.
Now we can sketch the asymptotes and the vertices, remembering to shift everything so that the center is (2, -3):
Asymptotes, and vertices (-4,-3) and (8,-3).
Now for the hyperbola:
"East-West" hyperbola (in green) with its asymptotes (in magenta color).
3. We could expand our equations for the hyperbola into the following form:
`Ax^2+ Bxy + Cy^2+ Dx + Ey + F` ` = 0` (such that `B^2>4AC`)
In the earlier examples on this page, there was no xy-term involved. As we saw in Example 5, if we do have an xy-term, it has the effect of rotating the axes. We no longer have "north-south" or "east-west" opening arms - they could open in any direction.
Example 7 - Hyperbola with Shifted and Rotated Axes
The graph of the hyperbola x2 + 5xy − 2y2 + 3x + 2y + 1 = 0 is as follows:
Shifted and rotated hyperbola.
We see that the axes of the hyperbola have been rotated and have been shifted from `(0, 0)`.
[Further analysis is beyond the scope of this section. ]
Exercise
Sketch the hyperbola
`x^2/9-y^2/16=1`
Answer
This is an east-west opening hyperbola, with a = 3 and b = 4. It will look similar to the east-west opening Example 3, given above.
x-intercepts: Letting y = 0 in the equation given in the question, and we have:
`x^2/9=1`
Solving gives us:
x = -3 and x = 3
Aymptotes: We have an east-west opening hyperbola, so the slopes of the asymptotes will be given by
`+-b/a`
In this example, a = 3 and b = 4. So the slopes of the asymptotes will be simply:
`-4/3` and `4/3`.
The equations for the asymptotes, since they pass through `(0, 0)`, are given by:
`y = -(4x)/3` and `y = (4x)/3`
Including the above information on our graph:
Asymptotes (in magenta color) and vertices.
Completing the hyperbola:
"East-West" hyperbola (in green) with its asymptotes (in magenta color).
Conic section: Hyperbola
How can we obtain a hyperbola from slicing a cone?
We start with a double cone (2 right circular cones placed apex to apex):
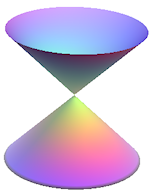
When we slice the 2 cones vertically, we get a hyperbola, as shown.
