Singapore wealth - mean and median?
By Murray Bourne, 12 Oct 2010
Singapore has rapidly developed into a wealthy country during the last 50 years.
In a recent Straits Times article, "Singaporeans ranked 4th for personal wealth" (Sat 9th Oct 2010, article no longer available), journalist Gabriel Chen writes:
Singaporeans are the fourth richest people in the world in terms of personal wealth [with an average adult wealth of US$255000] and second richest in Asia-Pacific, according to a Credit Suisse report.
[Singapore is] behind Switzerland (US$372,692), Norway (US$326,530) and Australia (US$320,909), but ahead of major developed economies like France, the United States and Britain in the Swiss bank's inaugural Global Wealth Report, out yesterday. [...]
"Wealth" is defined as "real" assets (like housing) plus cash and investments minus debt.
Now, the next sentence caught my eye (emphasis is mine):
While Singapore's mean wealth of US$255,488 is extremely high, its median wealth is approximately just one-ninth of that, at US$30,092 per adult. Median refers to the wealth for the "middle" of the adult population distribution here, while mean is the average.
This raises some interesting issues, one of which is mentioned in the article:
While the disparity between median and average wealth here seems to imply a high level of wealth inequality, DBS economist Irvin Seah disagrees.
It certainly does imply such inequality. In an earlier article, I pointed out that Singapore's Gini Coefficient (a measure of wealth equality) is quite high, indicating a fairly poor distribution of wealth. Singapore's Gini Coefficient comes somewhere between China's and the USA's.
Back to the article. I was not sure about this next conclusion, so I decided to investigate it:
The findings suggest most of the wealth is accumulated around the middle to upper-middle income group, with "most Singaporeans doing better than their peers in other countries", Mr Seah said.
If the wealth were normally distributed, then we would expect the graph of the situation to look like the following, with the mean (average), median (mid-point, where 1/2 of the population is above and half is below that figure) and mode (the most-often occurring wealth figure) all being equal to $250,000 (in round figures).
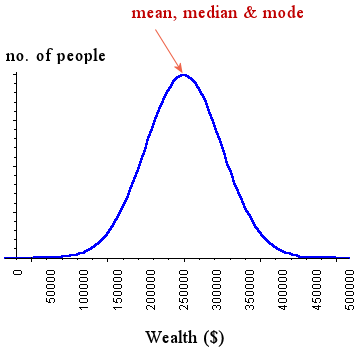
However, according to the article, the median is around $30,000. What will the graph look like now?
It turns out it will look something like this (where each class interval is $20000 wide, and the first mid-point is $10,000):
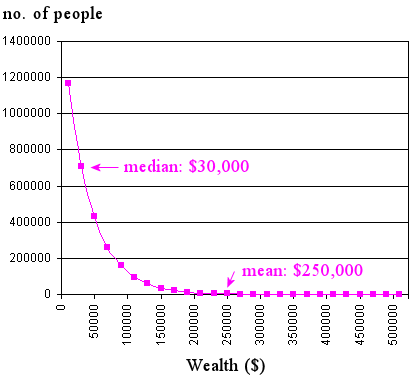
I'm assuming, of course, that no one has wealth beyond $500,000 so that my graph is readable. This is not the case and there are quite a few millionaires in Singapore. I'm also assuming there are around 3 million adults in Singapore.
Our graph shows the distribution is (heavily) skewed to the right.
So yes, Singapore has quite a high proportion of quite wealthy people, but don't miss that very large number of people (over a million) in the $0 to $20,000 interval. There are many battlers in Singapore.
See the 17 Comments below.
16 Oct 2010 at 4:57 pm [Comment permalink]
[...] net worth : US $255,488 but the median is only US $30,092. Square circle Z has already tried to analyse it, so I shall not say much [...]
4 Jul 2011 at 12:40 pm [Comment permalink]
This article can be interpreted as extremely misleading. While mean is a very accurate way to determine the average of certain things and statistics, it can also be very misleading. You have to take a good, long look at the median and mode just to gain a correct perspective on the data. While Singapore's mean wealth is US$255,488, the median wealth is one-ninth of that (around US$30,000). This means that most of Singapore's people are in the range of 0-20,000 US dollars, while a very select few may be extremely rich there. These statistics show that you have to take mean, median, and mode all into consideration, not just one of them.
4 Jul 2011 at 2:00 pm [Comment permalink]
@Logan - Yes, that was the point I was making, exactly!
26 Aug 2011 at 1:55 am [Comment permalink]
This article is misleading because while the mean can be a great way to determine the way the graph is going you have to include the mode and median because they are pretty important to the data set as well. This article only uses the mean to prove that the average person in Singapore is pretty wealthy. You have to consider the mode and median and well because they can be used to interpret the data as well. If the mean is $255,488 and the median is only one-ninth of that, that means that most of the people living in Singapore live within a wealth range of 0-20,000 US dollars. If the data is normally distributed then it looks symmetrical but if you distribute it based on the median then it is skewed a lot to the right. You have to wonder which graph is the right one because that is also pretty misleading.
26 Aug 2011 at 2:00 am [Comment permalink]
@Logan McCauley- Its a good review of the article but you probably have mentioned something about the graphs
30 Nov 2011 at 12:39 pm [Comment permalink]
The statistics showed that the mean was $255,488, a relatively high amount that would lead a person to conclude that the average income in Singapore is quite high. However, the data was not a normal distribution, causing the statistics to be skewed. In reality the mean is the least accurate way to deduce the average income in Singapore, because there are a few incredibly high incomes that outweigh the small incomes and cause the mean to be very high.
If normally distributed, the statistics would not be misleading. The distribution would show that one half of the population has a income greater than $255,488, leading one to correctly conclude that many people in Singapore are very wealthy.
The median would give the most accurate reflection of Singapore’s true wealth, due to the fact that when listing everyone’s income smallest to greatest, the middle number would better represent a more realistic value for the class of data.
30 Nov 2011 at 12:46 pm [Comment permalink]
Gregory Evans- I agree that the mean is a misleading way to portray the statistics, but I also think the mode is misleading.
6 Aug 2012 at 10:00 am [Comment permalink]
The use of statistics in this article are incredibly misleading, because the national mean (average) wealth information is skewed by the incredibly wealthy, a huge minority in the country. This minority gives the illusion that the majority (who actually averages about US$225,000 less than the original article suggests) makes more per person than what the median (the "middle" in a set of data, and what more closely resembles what the average Singaporean earns) concludes.
If the wealth was normally distributed, then the statistics would not be misleading, because the mean and the median of personal wealth would be equal. This would mean that the average wealth would more closely resemble the US$255,488 mark.
Using the median in this case would more closely resemble Singapore's true wealth, because this will give a more accurate view of the "true" average wealth in the country. This will also make sure that the extreme highs and lows will not skew the results.
6 Aug 2012 at 10:11 am [Comment permalink]
@Logan McCauley- I agree with you that focusing on "only one" of those three measures of central tendency can lead to misleading results, but focusing on the mode can be just as inaccurate as the mean.
26 Jan 2013 at 2:23 am [Comment permalink]
My thoughts are that the graph isn't misleading as people think it is. The first graph yes, the one that states the mean value. But in reality people in singapore are really poor. The mode interval in the second graph is inbetween 0 and 20000. Which gives us the idea that most people in singapore are lower class families. The group of millionaires that are in the 1% are skewing the graph to the right tremendously. They make up most of the money in the graph. However the median is a more accurate number that describes the working and lower class familes of singapore.
14 Mar 2013 at 7:58 am [Comment permalink]
This article is very misleading because in order for it to not be misleading, it would need to consider not only the mean of the population wealth data but also consider the median and mode of the population wealth data. Considering that the mean is $255,000 and the median is one-ninth of that, shows that the mean is not a good representation of the data shown in the article. If we were looking at a normal distribution, the data would not be misleading and it would be a better representation of the data given. it would not be misleading because $255,000 would be in the middle of the distribution which would also be the median of the data. Since the distribution is skewed to the right, the median would be a more accurate representation of the data because it is the middle of the data. There would be half of the population above the median and half below giving a more accurate representation.
1 May 2014 at 4:54 pm [Comment permalink]
[…] Singapore wealth - mean and median? :: squareCircleZ if the wealth distribution of singapore is as such, then the majority of singaporeans are poor. note that the number of top most earners are neglible and how much they earn is none of the nation's concern. the higher income group of the majority population is therefore about 100k, giving a monthly population of 8k, and for these "high" income group to clear the debt of financing a house using 25% of monthly income in 5 years time, they can only afford 120k which is hell far off from a 5 room flat or small condo, costing anywhere from 600k to 1.5 million. __________________ Be Kind whenever possible. It is always possible. Peekture taken at Dubrovnik, Croatia […]
7 Jul 2014 at 2:49 pm [Comment permalink]
This article can be very misleading because, although mean is a good way to find the average you also must look at the median and the mode as well. The article only tries to prove its point with the mean. The mean is $255,488 but the data is not in a normal distribution so the data is skewed. The mean does not resemble Singapore's wealth and is the most inaccurate way to show the data, while the median would have been the most reasonable/accurate way to show the data.
7 Jul 2014 at 3:02 pm [Comment permalink]
@Layne: More than half of the article states why mean is not the most suitable measure in this case, and the graphs back up the point. So it already does "look at the median and the mode as well".
6 Jul 2015 at 2:49 pm [Comment permalink]
This article is misleading because the first graph is incomplete and does not show the number values on one side, so it is impossible to figure out if the graph is correct or not. If the wealth had been normally distributed it would not have been anywhere near as misleading as it is, it wouldn't be misleading because the mean and median would be equal. Using the median would give a better view and understanding of the wealth of the city's people. Since most of the people in the city are lower class they don't have as much wealth, and they represent the mass of the city.
6 Jul 2015 at 3:16 pm [Comment permalink]
Tiffany Fox- I agree with what you're saying and the points you made but maybe you could have gone deeper into detail and maybe mentioned something about the graphs.
7 Jul 2015 at 7:30 pm [Comment permalink]
As mentioned in the article, the first graph is an ideal situation where the mean, mode and median equal each other.
There is no point putting any values on the vertical axis, since this is not a realistic, but ideal graph.