Baseball bat math

There is some interesting mathematics behind baseball bats.

In a paper on baseball bat physics by Larry Noble, it says:

During the swing, the maximum linear (COP) and rotational velocity of the bat is approximately 33 m/s and 36 r/s, respectively, for college females and 38 m/s and 44 r/s, respectively, for college males.

Some explanations:

"COP" means "center of percussion".
m/s is meters/second
r/s is radians per second

[You can read about linear and rotational (or angular) velocity at Applications of Radian Measure.]

The COP is important because:

When the ball hits the bat at the center of percussion (COP), there is no reaction impulse (shock) at the axis. The impact axis for bats has been shown to be the point under the first knuckle of the top hand.

The paper goes on to describe differences in resonant frequency characteristics between wooden bats and hollow-wall aluminium (aka "aluminum") bats. There is also an analysis of the overtones set up in the bat during the swing:

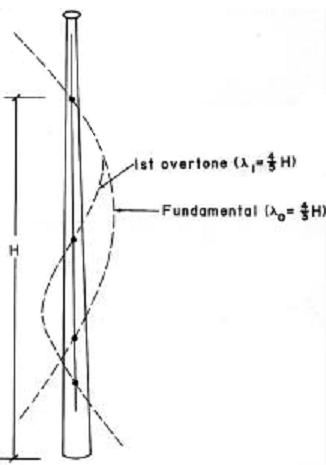
During impact, the vibration behavior of the bat corresponds to that of a free, non-supported bat [...] irregardless of the firmness of the grip.

One of the problems identified in the paper:

Because the primary goal of the power swing is to maximize bat velocity on impact, it is somewhat surprising that maximum bat velocity has repeatedly been found at from .01 to .05 s prior to impact

The paper's conclusion:

The most important mechanical properties of the bat are: (1) mass, (2) moment of inertia, (3) coefficient of restitution (COR), (4) vibrational properties, (5) center of percussion location (COP), and (6) maximum power point location.

The paper involves other applications of mathematics, including:

• Calculus
• Statistics
• Trigonometry
• Functions
• Geometry

Hoop Frequency

In another paper, Hoop Frequency as a predictor of performance for softball bats, by D. Russell at Kettering University (which is no longer available) we learn that:

Hollow metal and composite baseball and softball bats exhibit two types of vibrational modes, bending modes and hoop modes. The hoop modes are unique to hollow bats and involve only a radial vibration of the barrel of the bat. The lowest frequency hoop mode is responsible for both the "ping" sound of a metal bat and the so-called "trampoline effect".

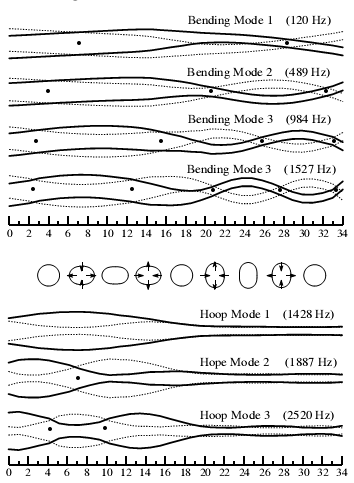
Diagram shows bending mode and hoop mode of a baseball bat. Dots represent nodes.

There are many interesting applications of mathematics in this paper as well:

• Differential equations
• Statistics
• Trigonometry

Baseball bats are an interesting mathematical study. We should start math lessons with such applications and draw the theory from it, rather than trying to rush through applications at the end of a lesson.

See the 1 Comment below.