Number Sense
By Murray Bourne, 11 Aug 2010
You may have seen Maggie, the dog who can count:
Humans (as well as many animal species) are born with a "number sense", according to Stanislas Dehaene in his book The Number Sense - How The Mind Creates Mathematics.
This means we already have a "feel" for number quantities long before our parents teach us, or before we ever go to school. And animals also have a limited number sense, but not quite as sophisticated as that demonstrated by Maggie in the above video. (Actually, Maggie can't really count. What's going on there is what is known as the "Hans Effect". See Clever Hans.)
As is often the case, the reality is more remarkable than the fiction. Animals can certainly count, and just like us, they are much better with smaller numbers (1, 2, 3) but become more vague and prone to error as the numbers get larger (4 and onwards).
Counting vs Subitizing
Look at these 2 pictures. How many circles are there in each?


Now think about how you counted the circles.
For the left one, you most likely just looked and immediately concluded "3", but for the one on the right, you most likely had to count them one-by-one to make sure you got the correct number, right?
In the case where we know the number of objects without individually counting them, we are said to be "subitizing", a term coined in the late 1940s by E. L. Kaufman and others.
(See how fast your own counting ability is: Counting Challenge. It's easy - you just need to count the dots as fast as you can.)
We share this subitizing ability with many animals.
Animal Math
A rat can be trained to pull a lever a set number of times to get a food reward. It "knows" there is a difference between 2 pulls and 3 pulls, and soon gets plenty of reward for the correct number of pulls. But if the required number of pulls increases, the rat becomes increasingly innacurate and tends to pull the lever random times in the hope of being correct.
Similarly, chimpanzees can tell the difference between the number of objects in different piles. An interesting observation is that the chimp can easily tell that 6 objects is "more" than 2 objects, but commits more errors when trying to compare 5 objects with 6 objects. This is called "distance effect" and the task becomes even more difficult when the number of objects increases (for example comparing 9 and 10 is much more difficult for the chimp than comparing 1 and 2 objects, even though the difference between them is the same). This is called the "magnitude effect".
It is the same for us. We can easily tell the difference between small groups of objects (or a small group compared to a large group), but we have difficulty comparing 2 large groups, since we can only be sure of our conclusion if we count them one-by-one.
Babies, too
What is interesting is that babies who are just a few days old exhibit subitizing. That is, they can distinguish between different numbers of objects and sounds. The way psychologists test this is to sit the babies on their mothers' laps and repeat sounds over and over. If the sounds consist entirely of 2-syllable words, the baby becomes bored quite quickly, but if a 3-syllable word is inserted, the baby immediately becomes attentive again. This demonstrates that babies can "count", at least in a rudimentary way.
1, 2, 3, many...
Let's go back to the simple task of counting dots, like in my 2 pictures earlier.
Since the 1880s, psychologists have known that counting 1, 2 or 3 objects was very quick and very accurate (subitizing), but for counting larger groups of objects, the amount of time required and the number of errors increases dramatically.
In the following chart, we see the result of getting people to count dots as quickly as they can. For 1, 2 and 3 dots, the time required is around 0.6 of a second, whereas there is a linear increase from there to 6 dots. There is a similar increase in the error rate.
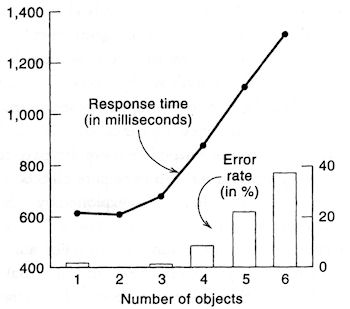
Source: The Number Sense, p 67.
One explanation for the above results is that we perceive 1, 2 or 3 objects using a "parallel processor", but we need to use a different serial mechanism to keep track of higher numbers of objects.
Number and Language
Consider for a moment how languages deal with 1, 2 and 3 differently from the rest of the numbers.
In English, for example, we use "th" and say fourth, fifth, sixth and so on for all the ordinal numbers therafter. But we have different endings for the first 3 ordinals: first, second, and third.
In some tribal languages, the only numbers used are "one", "two", "three" and "many".
So what is "Number Sense"?
Number sense involves being aware and having a reasonable understanding of the following concepts:
- The differences between numbers and their symbols
- Numbers as used to describe:
- How many (cardinal e.g. "5 cats");
- The order of things or events (ordinal, e.g. "the 5th book from the left"); and
- The name or identity of something (nominal e.g. "his phone number is 9226-7841")
- The relationship between numbers (big-small, before-after). The concept of number line is important here.
- The effects of operating on numbers (adding, subtracting, etc)
- Estimation and rounding
- Being able to use relationships between numbers to simplify calculations (e.g. 79 + 45 = 80 + 45 − 1 = 125 − 1 = 124)
There are some really interesting cases where people have suffered from some brain trauma and have lost their "number sense", or perhaps their ability to count. They will be able to get up to 3 just fine, but lose track very quickly after that.
Further Reading
I recommend:
- The Number Sense - How The Mind Creates Mathematics by Stanislas Dehaene. (You can see some of it via Google Books)
-
Teaching Mathematical Concepts
(This was actually a resource for teaching blind children, but has since disappeared.)
Activity
As mentioned earlier, see how fast you can count: Counting Challenge. You've got 10 seconds for each round.
See the 3 Comments below.
12 Aug 2010 at 12:28 am [Comment permalink]
This answers a lot of questions regarding on the calculative abilities of babies, so this means that the brain has in them from birth for maths. This is interesting in many ways. Thanks you for sharing this with us
6 Nov 2010 at 5:15 am [Comment permalink]
My dog is teached to bark when I show him fingers. On one finger it barks once. On two fingers it barks twice and so on. Yes, you are right - on more than three the errors are much.
Now it's time time (however) to let you know that in this dog counting there is a little trick. The trainer actually helps the dog a lot. If I show only one finger to the dog it will bark once. However if I keep the finger raised and shake it very little - it will bark twice.
I use this for error correction. For example when I show to the dog three fingers and it bark twice only, I do a little move with the fingers and it knows that it was mistaken, so it barks one more time. Usually this remains hidden for the people who are watching the trick.
So briefly - yes, the dogs are counting; however the errors are lots even with the small numbers. The reason is that they count for food; however the food is something that makes their nerve system too tensely. They do not think in full power on food conditions 🙂 I know that they can do much more 🙂
6 Nov 2010 at 4:51 pm [Comment permalink]
Ahh, Philip, so you are doing one more step than the Hans Effect, by deliberately giving helpful cues. Thanks for sharing.