7. Work by a Variable Force using Integration
by M. Bourne
The work (W) done by a constant force (F) acting on a body by moving it through a distance (d) is given by:
W = F × d
Example of work done by a constant force

An apple weighs about `1\ "N"`. If you lift the apple `1\ "m"` above a table, you have done approximately `1\ "Newton meter (Nm)"` of work.
Work done by a Variable Force
If the force varies (e.g. compressing a spring) we need to use calculus to find the work done.
If the force is given by F(x) (a function of x) then the work done by the force along the x-axis from a to b is:
`W=int_a^bF(x)dx`
Hooke's Law for Springs
The force (F) that it takes to stretch (or compress) a spring x units from its normal length is proportional to x.
`F = kx`
We can find the spring constant k from observing what force gives what stretch for each spring. This spring constant is also called the stiffness of the spring.
Interactive Appplet
In this activity, you can see the forces involved, the work done and you can explore the meaning of k, the spring constant.
Things to do...
- Extend or compress the spring by dragging the mass. See the force required to do this. (You can drag the mass when it goes green.)
- When you let go, you will see the work done in compressing or extending the spring.
- Change the value of k using the slider and see how much this changes the force required and the work done.
- Why does the force increase as the amount of stretch (x) increases?
- Does the relationship `F = kx` hold?
- Why does the spring slow down?
Natural length of spring = 100 cm
Spring constant, k = N/cm
Stretch/compression = cm
Force = N
Work = N cm
Copyright © www.intmath.com Frame rate: 0
NOTE: The above activity assumes we are looking at the spring from above and it's moving horizontally.
You can see other interesting spring examples at Applications of Trigonometric Curves and in Composite Trigonometric Curves.
Example 1
(a) Find the work done on a spring when you compress it from its natural length of 1 m to a length of 0.75 m if the spring constant is k = 16 N/m.
Answer
The force when the spring is extended (or compressed) by `x` units is given by:
`F = 16x`
We start compressing the spring at its natural length (0 m) and finish at 0.25 m from the natural length, so the lower limit of the integral is 0 and the upper limit is 0.25. So:
`"Work"=int_0^0.25 16x\ dx`
`=[8x^2]_0^0.25`
`=0.5\ text[N. m]`
(b) What is the work done in compressing the spring a further 30 cm?
Answer
This time, we start pushing the spring at 0.25 m from the natural length and finish at 0.55 m from the natural length, so the lower limit of the integral is 0.25 and the upper limit is 0.55.
`"Work"=int_0.25^0.55 16x\ dx`
`=[8x^2]_0.25^0.55`
`=1.92\ text[N.m]`
Note: For a spring,
`W = int_a^b F(x)dx`
requires that a and b are the distance from the natural position of the spring.
Example 2
A force of 1200 N compresses a spring from its natural length of 18 cm to a length of 16 cm. How much work is done in compressing it from 16 cm to 14 cm?
Answer
We must work out the spring constant first (we will work in cm).
`F = kx`
So `1200 = k(2)`
So `k = 600\ "N/cm"`
So in this case,
`F = 600x`
Now the work done is given by:
`"Work"=int_2^4 600x\ dx`
`=[300x^2]_2^4`
`=3600 text[ N. cm]`
Check your understanding
Go back up to the spring interactive above and calculate the work done in compressing or stretching the spring for various amounts of stretch. Do your answers tally with the answer given?
Let's now look at another example of work done by a variable force.
Example 3
Need Graph Paper?
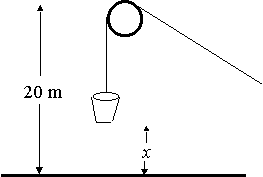
A leaky bucket weighing 5N is lifted 20 m into the air at a constant speed. The rope weighs 0.08 Nm-1. The bucket starts with 2 N of water and leaks at a constant rate. It finishes draining just as it reaches the top. How much work was done:
a) lifting the water alone
Answer
a) Water only.
The force required to lift the water is the water's weight.
When the bucket is x metres off the ground, the expression for the water's weight can be found by first graphing it:
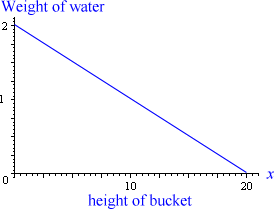
So, using y = mx + c, we see that the slope is
`m = -2/20 = -1/10` and
the y-intercept is `c = 2`
So we can write the function for the weight at height x as:
`F(x)=-x/10 + 2`
Then
`"Work"=int_a^bF(x)\ dx`
`=int_0^20(-x/10+2) dx`
`=[-(x^2)/(20)+2x]_0^20`
`=-20+40`
`=20 text[ N.m (20 joules)]`
Alternatively, we could have found the function as follows:
`F(x) = 2(20-x)/20 "N"`
where `2` is the original weight of the water, and `(20-x)/20` is the proportion of water left at height `t`.
This simplifies to `F(x)=(2-x/10)\ "N"`.
b) lifting the water and bucket together
Answer
b) Water and bucket
For the bucket,
`W = Fd`
`= 5 × 20`
`= 100\ "N.m"`
So total work `= 20 + 100 = 120\ "N.m"`
c) lifting the water, bucket and rope?
Answer
c) Water, bucket, rope
The weight of the rope at height x is:
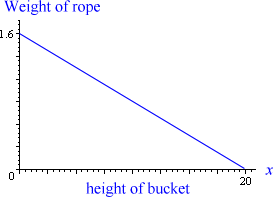
`F(x) = 0.08(-x + 20)`
The work done on the rope is:
`int_0^20 0.08(-x+20) dx`
`=0.08[-(x^2)/(2)+20x]_0^20`
`=-16+32`
`=16\ text[N.m]`
So the total work done on the water, bucket and rope is
`W` `=(20 + 100 + 16)\ "N.m"` `= 136\ "N.m"` (or `136\ "J"`).