10. Force Due to Liquid Pressure by Integration
by M. Bourne
The force F on an area A at a depth y in a liquid of density w is given by
`F = wyA`
The force will increase if the density increases, or if the depth increases or if the area increases.
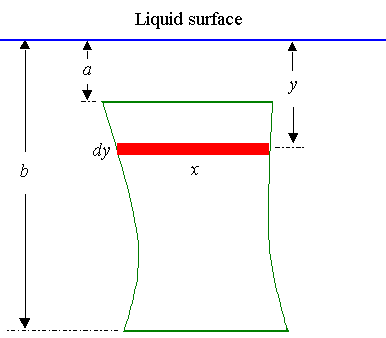
So if we have an unevenly shaped plate submerged vertically in a liquid, the force on it will increase with depth. Also, if the shape of the plate changes as we go deeper, we have to allow for this.
So we have:
Now, the total force on the plate is given by
`F=wint_a^bxy\ dy`
where
x is the length (in m) of the element of area (expressed in terms of y)
y is the depth (in m) of the element of area
w is the density of the liquid (in N m-3)
(for water, this is w = 9800 N m-3)
a is the depth at the top of the area in question (in m)
b is the depth at the bottom of the area in question (in m)
Example 1
Find the force on one side of a cubical container `6.0` cm on an edge if the container is filled with mercury. The weight density of mercury is `133` kN/m3.
Answer
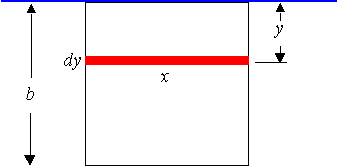
This is the same as having a square plate of sides 6.0 cm submerged in mercury.
This is a very basic example where the width of the plate does not change as we move down the plate.
It is always `x = 6`.
Also, the depth of the top of the plate is 0, so `a = 0`.
To apply the formula, we have:
`x = 0.06\ "m"``y` is the variable of integration
`w = 133\ "kN m"^-3= 133,000\ "N m"^-3`
`a = 0``b = 0.06`
So we have:
`"Force"=w int_a^b xy\ dy`
`=133000 int_0^0.06 0.06y\ dy`
`=7980 int_0^0.06\ y\ dy`
`=7980[(y^2)/(2)]_0^0.06`
`=14.4\ text[N]`
Example 2
A right triangular plate of base `2.0` m and height `1.0` m is submerged vertically in water, with the top vertex `3.0` m below the surface.
Find the force on one side of the plate.
Answer
Before we can proceed, we need to find x in terms of y.
Now when `x = 0`, `y = 3` and when `x = 2,` `y = 4`.
So we have:
`y=mx+c`
`=1/2x+3`
This gives us `x = 2y − 6`.
To apply the formula, we have:
`x = 2y − 6 = 2(y − 3) ``y` is the variable of integration
`w = 9800\ "N m"^-3``a = 3`
`b = 4`
So we have:
`"Force"=wint_a^bxy\ dy`
`=9800 int_3^4 2y(y-3)\ dy`
`=19600 int_3^4 (y^2-3y) text[d]y`
`=19600 [(y^3)/(3)-(3)/(2)y^2]_3^4`
`=19600[((4^3)/(3)-3/2(4)^2)` `{:-((3^3)/(3)-3/2(3)^2)]`
`=19600[-2.667 - (-4.5)]`
`=35900\ text[N]`