Which is the correct graph of arccot x?
By Murray Bourne, 03 May 2011
A reader challenged me on the graph I had for y = arccot x, on the page Inverse Trigonometric Functions.
He wrote (in a rather unfriendly tone):
Compare:
https://en.wikipedia.org/wiki/Inverse_trigonometric_functions
https://www.intmath.com/analytic-trigonometry/7-inverse-trigo-functions.php
You incorrectly state the range of the arccotangent function as -pi/2 to pi/2. It is not. The correct range of arccotangent is 0 to pi.
After some deliberation, I have now included both interpretations on my page, because both are found in various sources.
First, some background.
Obtaining the graph of y = arccot(x)
The graph of y = arccot x can be obtained from a consideration of the graph of y = cot x.
But depending on your starting region, you'll get a different graph for y = arccot x.
Interpretation 1
The graph of y = cot x is as follows:
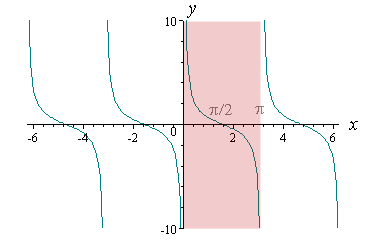
We choose the portion from x = 0 to x = π (as highlighted above), and reflect it in the line y = x like this.
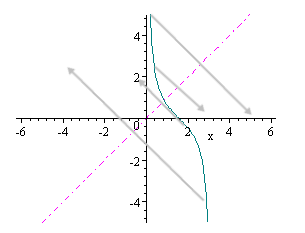
Since reflection in the line y = x gives us the inverse of a function, we have obtained the graph of y = arccot x, as follows:
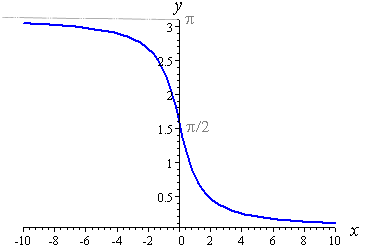
From the graph we can see the domain (the possible x-values) of y = arccot x is:
All values of x
And the range (resulting y-values) of arccot x is:
0 < arccot x < π
If we evaluate our function for some negative value of x, say x = −2, then we get a positive answer, as expected from the graph:
arccot(−2) = 2.678...
Alternate View - Interpretation 2
Some math textbooks (and some respected math software, e.g. Mathematica) regard the following as the region of y = cot x that should be used (that is, −π/2 to π/2):
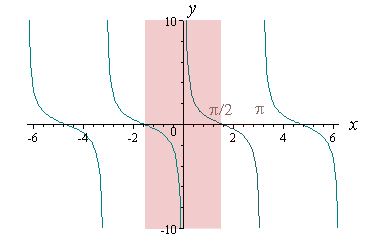
This would give the following discontinuous graph when reflected in the line y = x:
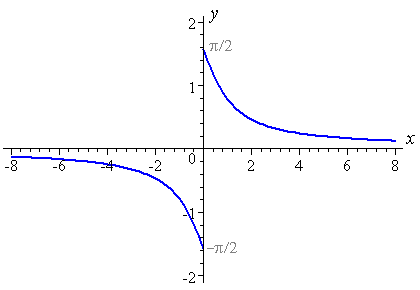
So the domain of arccot x would be (as for Interpretation 1):
All values of x
Using this interpretation, the range of arccot x would be:
−π/2 < arccot x ≤ π/2 (arccot x ≠ 0)
If this is the correct graph, we expect a negative answer when we evaluate the function at x = −2. It is actually:
arccot(−2) = −0.46365...
Which is correct?
According to a response to a reader's question on this same issue, Dr. Math goes for the first interpretation:
In order to invert a trig function, we first restrict it to a domain on which it takes all its possible values, once each; then we invert the restricted function, whose range is then that restricted domain.
Look at a graph of the cotangent function, and you will see that although between -pi/2 and pi/2 it takes all its possible values, and takes each value only once, there is one problem with this choice: it is not continuous (or even defined) on this entire domain, but is undefined at 0.
The domain would then have to be
-pi/2 < x < 0 or 0 < x <= pi/2
To avoid this, we instead choose the domain
0 < x < pi
which is cleaner to work with, making a continuous function defined over the entire domain.
Math software doesn't agree, either
Let's now see the inconsistent way (respected) math software deals with this function.
Mathcad's Interpretation
When I graphed the function acot(x) in Mathcad, this is the result (they are using the first interpretation):
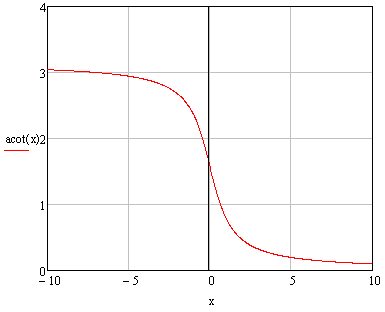
Mathcad gives arccot(−2) = 2.678..., which is consistent with their graph. Mathcad uses "acot(x)" notation.
Mathematica's Interpretation
However, according to Mathematica (using Wolfram|Alpha) , this is the graph of y = arccot(x):
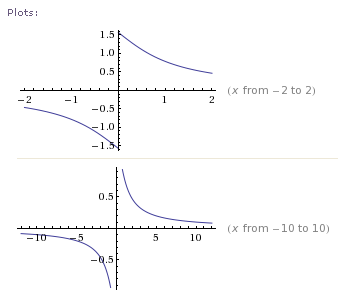
So Mathematica is using the second interpretation of the function. (They use the somewhat poor notation y = cot−1x.)
Taking a typical value, Mathematica (Wolfram|Alpha) gives us
arccot(−2) = −0.46365...
How can this be? The first interpretation gives us a positive value for arccot(−2), while the second interpretation gives us a negative value.
Matlab's Interpretation
Matlab also gives us a discontinuous graph based on the second interpretation.
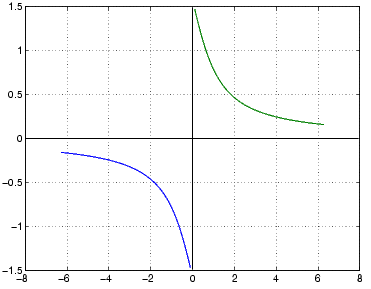
Matlab also uses "acot(x)" notation.
Maple/Scientific Notebook's Interpretation
My version of Scientific Notebook has both Maple and MuPAD engines. The results using both of these are curious.
Using the Maple engine, we get an answer using the first interpretation.
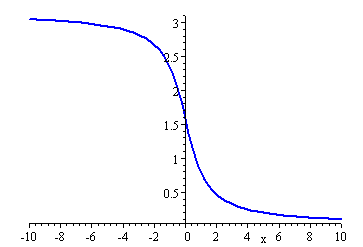
But when we switch to use MuPAD in Scientific Notebook, we get this result, which uses the second interpretation!
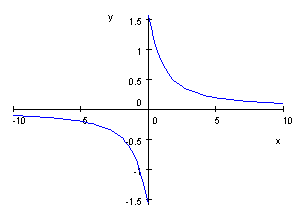
So even the top math software makers can't agree.
Conclusion
Here's another case where our math definitions are not as tight as we are often led to believe.
Also, the notation is inconsistent. Different text books and different software use the following to mean the same thing:
- arccot(x)
- acot(x)
- cot−1x
We should never use the last one! (See my rant on this here: Arcsin or sin?)
So which version of arccos(x) is the right one? Is my reader correct? (I don't know his name or email so I can't reply to him. Strange.)
I know which interpretation I think is "best". What are your thoughts?
See the 40 Comments below.
