Skip to main content
Interactive Mathematics
MATH SOLVER 🤖 Search
Search IntMath
Close

Interesting semi-logarithmic graph - YouTube Traffic Rank

By Murray Bourne, 25 Jan 2007

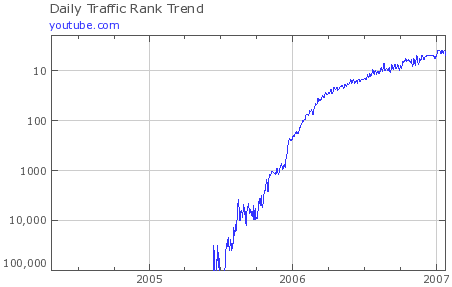
The growth in popularity of YouTube has been extraordinary. It has gone from an unknown, unheard-of site (not even in the top 100,000 sites, so off the scale) to the 5th highest ranked site on the Web, all in the space of 18 months.

This image, from Alexa, is an interesting example of a semi-logarithmic graph. The vertical scale (traffic rank) is logarithmic, while the horizontal scale (time) is linear.

YouTube

See the 7 Comments below.

Related posts:

  1. Twitter - dramatic growth in (older) traffic So you thought Twitter was just for kids? Think again....
  2. IntMath Newsletter: Cultural math, visual stats, matrices and persistence In this Newsletter: 1. Happy new multicultural year 2. Inverse of a matrix by Gauss-Jordan...
  3. A logarithmic music scale This musician's use of a logarithmic musical scale reminds me of my own 10-tone scale...
  4. Life expectancy and semi-log graphs A life table gives us an idea of how much longer we can expect to...
  5. Twitter follower semi-log graphs Here are some semi-log graphs showing Twitter follower (and following) numbers....

Posted in Mathematics category - 25 Jan 2007 [Permalink]

Tags: ,

Leave a comment




Comment Preview

HTML: You can use simple tags like <b>, <a href="...">, etc.

To enter math, you can can either:

  1. Use simple calculator-like input in the following format (surround your math in backticks, or qq on tablet or phone):
    `a^2 = sqrt(b^2 + c^2)`
    (See more on ASCIIMath syntax); or
  2. Use simple LaTeX in the following format. Surround your math with \( and \).
    \( \int g dx = \sqrt{\frac{a}{b}} \)
    (This is standard simple LaTeX.)

NOTE: You can mix both types of math entry in your comment.

top

Tips, tricks, lessons, and tutoring to help reduce test anxiety and move to the top of the class.