4. Multiplication of Matrices
Important: We can only multiply matrices if the number of columns in the first matrix is the same as the number of rows in the second matrix.
Example 1
a) Multiplying a 2 × 3 matrix by a 3 × 4 matrix is possible and it gives a 2 × 4 matrix as the answer.
b) Multiplying a 7 × 1 matrix by a 1 × 2 matrix is okay; it gives a 7 × 2 matrix
c) A 4 × 3 matrix times a 2 × 3 matrix is NOT possible.
How to Multiply 2 Matrices
We use letters first to see what is going on. We'll see a numbers example after.
As an example, let's take a general 2 × 3 matrix multiplied by a 3 × 2 matrix.
`[(a,b,c),(d,e,f)][(u,v),(w,x),(y,z)]`
The answer will be a 2 × 2 matrix.
We multiply and add the elements as follows. We work across the 1st row of the first matrix, multiplying down the 1st column of the second matrix, element by element. We add the resulting products. Our answer goes in position a11 (top left) of the answer matrix.
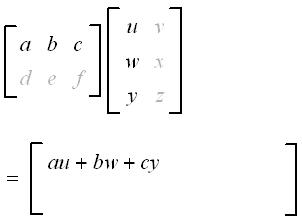
We do a similar process for the 1st row of the first matrix and the 2nd column of the second matrix. The result is placed in position a12.
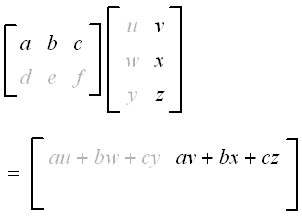
Now for the 2nd row of the first matrix and the 1st column of the second matrix. The result is placed in position a21.
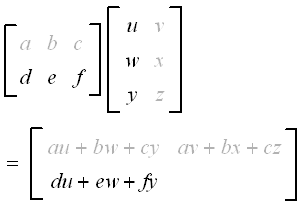
Finally, we do the 2nd row of the first matrix and the 2nd column of the second matrix. The result is placed in position a22.
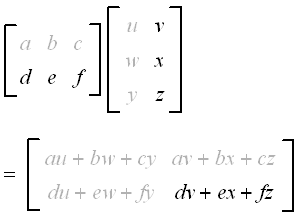
So the result of multiplying our 2 matrices is as follows:
`[(a,b,c),(d,e,f)][(u,v),(w,x),(y,z)]` `=[(au+bw+cy,av+bx+cz),(du+ew+fy,dv+ex+fz)]`
Now let's see a number example.
Phone users

NOTE: If you're on a phone, you can scroll any wide matrices on this page to the right or left to see the whole expression.
Example 2
Multiply:
`((0,-1,2),(4,11,2))((3,-1),(1,2),(6,1))`
Answer
This is 2×3 times 3×2, which will give us a 2×2 answer.
`((0,-1,2),(4,11,2)) ((3,-1),(1,2),(6,1))`
`=((0xx3+ -1xx1 + 2xx6,0xx-1+ -1xx2 + 2xx1), (4xx3+11xx1+2xx6,4xx -1 + 11xx2 + 2xx1))`
` = ((0-1+12,0-2+2), (12+11+12,-4+22+2))`
` = ((11,0),(35,20)) `
Our answer is a 2×2 matrix.
Multiplying 2 × 2 Matrices
The process is the same for any size matrix. We multiply across rows of the first matrix and down columns of the second matrix, element by element. We then add the products:
`((a,b),(c,d))((e,f),(g,h))` `=((ae+bg,af+bh),(ce+dg,cf+dh))`
In this case, we multiply a 2 × 2 matrix by a 2 × 2 matrix and we get a 2 × 2 matrix as the result.
Example 3
Multiply:
`((8,9),(5,-1))((-2,3),(4,0))`
Answer
` ((8,9),(5,-1))((-2,3),(4,0)) `
`= ((8 xx -2+9xx4,8xx3+9xx0),(5xx-2+ -1xx4,5xx3 + -1xx0))`
` = ((-16+36,24+0),(-10+ -4,15 + 0)) `
` = ((20,24),(-14,15)) `
Matrices and Systems of Simultaneous Linear Equations
We now see how to write a system of linear equations using matrix multiplication.
Example 4
The system of equations
−3x + y = 1
6x − 3y = −4
can be written as:
`((-3,1),(6,-3))((x),(y))=((1),(-4))`
Matrices are ideal for computer-driven solutions of problems because computers easily form arrays. We can leave out the algebraic symbols. A computer only requires the first and last matrices to solve the system, as we will see in Matrices and Linear Equations.
Note 1 - Notation
Care with writing matrix multiplication.
The following expressions have different meanings:
AB is matrix multiplication
A×B is cross product, which returns a vector
A*B used in computer notation, but not on paper
A•B dot product, which returns a scalar.
[See the Vector chapter for more information on vector and scalar quantities.]
Note 2 - Commutativity of Matrix Multiplication
Does `AB = BA`?
Let's see if it is true using an example.
Example 5
If
`A=((0,-1,2),(4,11,2))`
and
`B=((3,-1),(1,2),(6,1))`
find AB and BA.
Answer
We performed AB above, and the answer was:
`AB = ((0,-1,2),(4,11,2)) ((3,-1),(1,2),(6,1))`
` = ( (11,0),(35,20) )`
Now BA is (3 × 2)(2 × 3) which will give 3 × 3:
`BA= ((3,-1),(1,2),(6,1))((0,-1,2),(4,11,2))`
` = ((0-4,-3-11,6-2),(0+8,-1+22,2+4),(0+4,-6+11,12+2))`
` = ((-4,-14,4),(8,21,6),(4,5,14)) `
So in this case, AB does NOT equal BA.
In fact, for most matrices, you cannot reverse the order of multiplication and get the same result.
In general, when multiplying matrices, the commutative law doesn't hold, i.e. AB ≠ BA. There are two common exceptions to this:
- The identity matrix: IA = AI = A.
- The inverse of a matrix: A-1A = AA-1 = I.
In the next section we learn how to find the inverse of a matrix.
Example 6 - Multiplying by the Identity Matrix
Given that
`A=((-3,1,6),(3,-1,0),(4,2,5))`
find AI.
Answer
`AI = ((-3,1,6),(3,-1,0),(4,2,5)) ((1,0,0),(0,1,0),(0,0,1))`
`=((-3+0+0,0+1+0,0+0+6),(3+0+0,0+ -1+0,0+0+0),(4+0+0,0+2+0,0+0+5))`
` =((-3,1,6),(3,-1,0),(4,2,5))`
` =A`
We see that multiplying by the identity matrix does not change the value of the original matrix.
That is,
AI = A
Exercises
1. If possible, find BA and AB.
`A=((-2,1,7),(3,-1,0),(0,2,-1))`
`B=(4\ \ -1\ \ \ 5)`
Answer
`BA=(4\ \ -1\ \ \ 5)((-2,1,7),(3,-1,0),(0,2,-1))`
`=( -8+(-3)+0\ \ \ 4+1+10\ \ \ 28+0+(-5))`
`=(-11\ \ 15\ \ 23)`
AB is not possible. (3 × 3) × (1 × 3).
2. Determine if B = A-1, given:
`A=((3,-4),(5,-7))`
`B=((7,4),(5,3))`
Answer
If B = A-1, then `AB = I`.
`AB=((3,-4),(5,-7))((7,4),(5,3))`
`=((21-20,12-12),(35-35,20-21))`
`=((1,0),(0,-1))`
` !=I`
So B is NOT the inverse of A.
3. In studying the motion of electrons, one of the Pauli spin matrices is
`s=((0,-j),(j,0))`
where
`j=sqrt(-1)`
Show that s2 = I.
[If you have never seen j before, go to the section on complex numbers].
Answer
`s^2=( (0,-j),(j,0))((0,-j),(j,0))`
`=(( 0-j^2,0+0), (0+0,-j^2+0))`
`= ((1,0),(0,1))`
`=I`
4. Evaluate the following matrix multiplication which is used in directing the motion of a robotic mechanism.

`( (cos\ 60° ,-sin\ 60° ,0),(sin\ 60°, cos\ 60°,0),(0,0,1))((2),(4),(0))`
Answer
`( (cos\ 60° ,-sin\ 60° ,0),(sin\ 60°, cos\ 60°,0),(0,0,1))((2),(4),(0))`
`=((2(0.5)-4(0.866)+0),(2(0.866)+4(0.5)+0),(0+0+0))`
`=((-2.464),(3.732),(0))`
The interpretation of this is that the robot arm moves from position (2, 4, 0) to position (-2.46, 3.73, 0). That is, it moves in the x-y plane, but its height remains at z = 0. The 3 × 3 matrix containing sin and cos values tells it how many degrees to move.