3. Matrices

by M. Bourne

A matrix is simply a rectangular table of numbers written in either `(\ )` or `[\ ]` brackets. Matrices have many applications in science, engineering and computing.

Let's first see some of the typical problems that are solved using matrices. We will learn how to solve these later.

Applications of Matrices

a. Engineering: Forces in a bridge or truss

A typical statics problem is represented by the following:

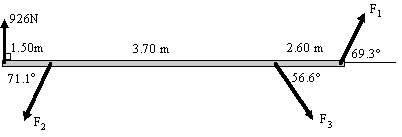
There are 3 unknown forces F₁, F₂, & F₃. From the diagram, we can obtain 3 equations involving the 3 unknowns and then solve the system using matrix operations.

We will see how to do this problem later, in Matrices and Linear Equations.

b. Electronics

The following circuit has 7 unknown currents marked I₁, I₂, I₃, I₄, I₅, I₆ and I₇.

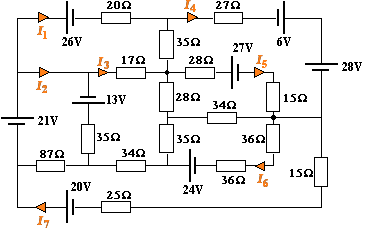
We can set up 7 equations involving the 7 unknowns and then use matrices to solve the system. We will see how to solve this later, also in Matrices and Linear Equations.

c. Other Applications of Matrices

Matrices is also used to solve problems in:

• genetics (working out selection processes)
• chemistry (finding quantities in a chemical solution)
• economics (study of stock market trends, optimisation of profit and minimisation of loss)

Now let's move on to matrix notation, some simple operations with matrices and some properties of matrices.

Matrix Notation

A matrix is written with ( ) or [ ] brackets.

Do not confuse a matrix with a determinant which uses vertical bars | |. A matrix is a pattern of numbers (or variables); a determinant gives us a single number.

The size of a matrix is written: rows × columns.

Examples of matrices

This is a 2 × 4 matrix. It has 2 rows and 4 columns.

`((2,4,-1,0),(1,3,7,2))`

This is a 4 × 1 matrix.

`[(4),(2.6),(-8.1),(7)]`

This is a 3 × 3 matrix. A matrix with the same number of rows and columns is called a square matrix.

`((1,2,3),(8,4,5),(4,-2,6))`

Elements in a matrix

The elements in a matrix A are denoted by a_ij, where i is the row number and j is the column number.

Example 1

Consider the matrix

`A=((5,4,9),(1,-2,3))`

The element `a_21=1`, since the element in the 2nd row and 1st column is 1.

The element `a_13=9`, since the element in the 1st row and 3rd column is 9.

Equality of Matrices

Equal matrices have identical corresponding elements.

Example 2

If

`((1,x),(y,3))=((1,2),(7,a))`

then `x = 2`, `y = 7` and `a = 3`.

Addition (and Subtraction) of Matrices

We can only add (or subtract) matrices if they have the same dimensions. That is, the two matrices must have the same number of rows and the same number of columns.

To add matrices, just add corresponding elements:

Example 3

` ((8,3,4),(0,-1,9) ) + ((5,-2,1),(6,3,5) )` ` =( (8+5, 3+ -2, 4+1) , (0+6,-1+3,9+5))` `=((13,1,5),(6,2,14))`

Note: We started with two matrices, both having dimensions 2 × 3. Our answer was also a 2 × 3 matrix.

See many more examples of matrix addition and subtraction in the Add & Multiply matrices applet.

Identity Matrix

The Identity Matrix, written I, is a square matrix where all the elements are 0 except the principal diagonal which has all ones.

Here is the 2 × 2 identity matrix:

`I=((1,0),(0,1))`

Here is the 3 × 3 identity matrix:

`I=((1,0,0),(0,1,0),(0,0,1))`

The identity matrix I is analogous to the number "`1`" in ordinary number multiplication. For example, if we multiply the number `8` by `1` (on either side), we have no change - the answer is still `8`.

`1 × 8 = 8 × 1 = 8 `

We'll see how matrix multiplication by the identity matrix works in the next section.

The identity matrix is also known as the unit matrix.

Diagonal Matrices

A diagonal matrix is a square matrix that has zeroes everywhere except along the main diagonal (top left to bottom right).

For example, here is a 3 × 3 diagonal matrix:

`[(7,0,0),(0,2,0),(0,0,-1)]`

Note: The identity matrix (above) is another example of a diagonal matrix.

Scalar Multiplication (and Division)

Scalar multiplication of matrices is similar to scalar multiplication of vectors. [For background, see Vector Concepts.]

We multiply (or divide) each element by the scalar value (a single number).

Example 4

If `A=((3,1),(7,-1),(2,8))`

then

`3A =3((3,1),(7,-1),(2,8)) = ((3xx3,3xx1),(3xx7,3xx-1),(3xx2,3xx8))` ` = ((9,3),(21,-3),(6,24))`

Note 1: When doing scalar multiplication, if we start with a 3 × 2 matrix, we end with a 3 × 2 matrix. This is not so in matrix multiplication that we meet in the next section.

Note 2: See many more examples of scalar multiplication in the matrix applet, which is on a following page.

Exercises

1. Find the value of the literal numbers (the variables):

`((x),(x+2),(2y-3))=((4),(y),(z))`

Answer

2. Find the sum of:

`((1,0,9),(3,-5,-2))+((4,-1,7),(2,0,-3))`

Answer