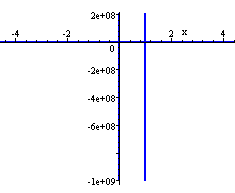7. Continuous and Discontinuous Functions
by M. Bourne
This section is related to the earlier section on Domain and Range of a Function. There are some functions that are not defined for certain values of x.
Continuous Functions
Consider the graph of f(x) = x3 − 6x2 − x + 30:
Graph of `y=x^3 - 6x^2 - x + 30`, a continuous graph.
We can see that there are no "gaps" in the curve. Any value of x will give us a corresponding value of y. We could continue the graph in the negative and positive directions, and we would never need to take the pencil off the paper.
Such functions are called continuous functions.
Functions With Discontinuities
Now consider the function `f(x) = 1/(x-1).`
We note that the curve is not continuous at `x = 1`.
Graph of `y=1/(x-1)`, a discontinuous graph.
We observe that a small change in x near `x = 1` gives a very large change in the value of the function.
For a function to be continuous at a point, the function must exist at the point and any small change in x produces only a small change in `f(x)`.
In simple English: The graph of a continuous function can be drawn without lifting the pencil from the paper.
Many functions have discontinuities (i.e. places where they cannot be evaluated.)
Example
Consider the function
`f(x)=2/(x^2-x)`
Factoring the denominator gives:
`f(x)=2/(x^2-x)=2/(x(x-1))`
We observe that the function is not defined for `x = 0` and `x = 1`.
Here is the graph of the function.
Graph of `f(x)=2/(x^2-x)`, a discontinuous function.
We see that small changes in x near 0 (and near 1) produce large changes in the value of the function.
We say the function is discontinuous when x = 0 and x = 1.
There are 3 asymptotes (lines the curve gets closer to, but doesn't touch) for this function. They are the `x`-axis, the `y`-axis and the vertical line `x=1` (denoted by a dashed line in the graph above).
Using computers to draw discontinuous graphs
Note: You will often get strange results when using Scientific Notebook (or any other mathematics software) if you try to graph functions which have discontinuities.
Here is the same function `f(x)=2/(x^2-x)` in the default graph view in Scientific Notebook:
It is showing us all the vertical values that it can (from an extremely small negative number to a very large positive number) - but we can't see any detail (certainly none of the curves).
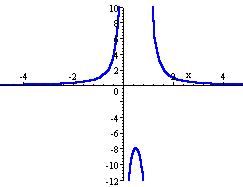
We need to restrict the y-values so we can see the true shape of the curve, like this (I have changed the view of the vertical axis from -12 to 10):
Continuity and Differentiation
Later you will meet the concept of differentiation. We will learn that a function is differentiable only where it is continuous.