4. Linear DEs of Order 1
If P = P(x) and Q = Q(x) are functions of x only, then
`(dy)/(dx)+Py=Q`
is called a linear differential equation order 1.
We can solve these linear DEs using an integrating factor.
For linear DEs of order 1, the integrating factor is:
`e^(int P dx`
The solution for the DE is given by multiplying y by the integrating factor (on the left) and multiplying Q by the integrating factor (on the right) and integrating the right side with respect to x, as follows:
`ye^(intP dx)=int(Qe^(intP dx))dx+K`
Example 1
Solve `(dy)/(dx)-3/xy=7`
Answer
`(dy)/(dx)-3/xy=7`
Here, `P(x)=-3/x` and `Q(x) = 7`.
Now for the integrating factor:
`"IF"=e^(intPdx)` `=e^(int-3/xdx` `=e^(-3 ln x)` `=e^(ln x^-3)` `=x^-3`
[If you are not sure what just happened, check out Integration: Basic Logarithm Form and Logarithms to Base e.]
We need to apply the following formula: `ye^(intPdx)=int(Qe^(intPdx))dx`
For the left hand side of the formula, we have
`ye^(intPdx) = yx^-3`
For the right hand of the formula, Q = 7 and the IF = x-3, so:
`Qe^(intPdx)=7x^-3`
Applying the outer integral:
`int(Qe^(intPdx))dx=int7x^-3dx =` `-7/2x^-2+K`
Now, applying the whole formula, `ye^(intPdx)=intQe^(intPdx)dx`, we have
`yx^-3=-7/2x^-2+K`
Multiplying throughout by x3 gives the general solution for `y`.:
`y=-7/2x+Kx^3`
Is it correct? Differentiate this answer to make sure it produces the differential equation in the question.
Here is the solution graph of our answer for Example 1 (I've used K = 0.5).
It is a cubic polynomial curve:
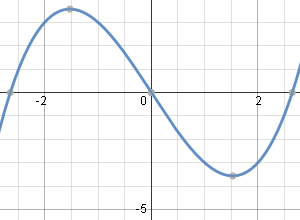
Solution using `K=0.5`.
Example 2
Solve `(dy)/(dx)+(cot x)y=cos x`
Answer
`(dy)/(dx)+(cot x)y=cos x`
Here, `P(x)=cot x` and `Q(x)=cos x`.
`"IF"=e^(intPdx)` `=e^(int cot x dx)` `=e^(ln sin x)` `=sin x`
(See Integration of Trigonometric Forms for an explanation of `int cot x dx`.)
Now `Qe^(intPdx)=cos x sin x`.
Apply the formula, `ye^(intPdx)=intQe^(intPdx)dx` to obtain:
`y sin x=intcos x sin x dx`
The integral needs a simple substitution: `u = sin x`, `du = cos x dx`
`y sin x=(sin^2x)/2+K`
Divide throughout by sin x to get the required general solution of the DE:
`y=(sin x)/2+K csc x`
Here is the solution graph of our answer for Example 2 (I've used K = 0.1) .
It is a composite trigonometric curve, where the main shape is the cosecant curve, and the "wiggles" are due to the addition of the (sin x)/2 part:
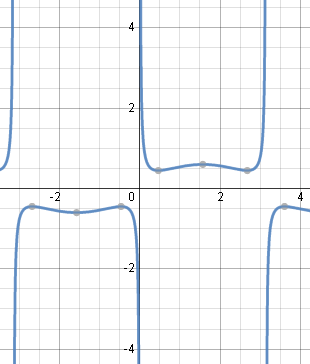
Typical solution graph using `K=0.1`.
Example 3
Solve `dy + 3y dx = e^(-3x)dx`
Answer
Dividing throughout by dx to get the equation in the required form, we get:
`(dy)/(dx)+3y=e^(-3x)`
In this example, P(x) = 3 and Q(x) = e−3x.
Now the integrating factor in this example is
`e^(intPdx)=e^(int3dx)=e^(3x)`
and
`intQe^(intPdx)dx=inte^(-3x)e^(3x)dx`
`=int1 dx`
`=x`
Using `ye^(intPdx)=intQe^(intPdx)dx+K`, we have:
ye3x = x + K
or we could write it as:
`y=(x+K)/e^(3x)`
Here is the solution graph for Example 3 (I've used K = 5).
It was necessary to zoom out (a lot) to see what is going on in this graph.
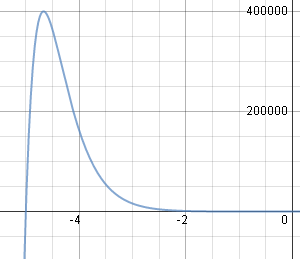
Typical solution graph using `K=5`.
Example 4
Solve `2(y - 4x^2)dx + x dy = 0`
Answer
We need to get the equation in the form of a linear DE of order 1.
Expand the bracket and divide throughout by dx:
`2y-8x^2+x(dy)/(dx)=0`
Rearrange:
`x(dy)/(dx)+2y=8x^2`
Divide throughout by x:
`(dy)/(dx)+2/xy=8x`
Here, `P(x)=2/x` and `Q(x) = 8x`.
`"IF"=e^(intPdx)` `=e^(int2/xdx)` `=e^(2 ln x)` `=e^(ln x^2)` `=x^2`
Now
`Qe^(intPdx)=(8x) x^2=8x^3`
Applying the formula:
`ye^(intPdx)=intQe^(intPdx)dx+K`
gives:
`y\ x^2=int8x^3dx+K=2x^4+K`
Divide throughout by x2:
`y=2x^2+K/x^2`
Solving directly, using Scientific Notebook
Scientific Notebook cannot solve our original question:
`2(y-4x^2)dx+x\ dy=0`
We have to rearrange it in terms of `(dy)/(dx)` and then solve it using
Compute menu → Solve ODE... → Exact
Here is the solution graph for Example 4 (I've used K = 5).
There is a discontitnuity at x = 0.
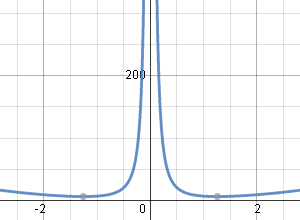
Typical solution graph using `K=5`.
Example 5
Solve `x(dy)/(dx)-4y=x^6e^x`
Answer
Divide throughout by x:
`(dy)/(dx)-4/xy=x^5e^x`
Here,
`P(x)=-4/x` and `Q(x)=x^5e^x`.
`"IF"=e^(intPdx)` `=e^(int-4/xdx)` `=e^(-4ln\ x)` `=e^(ln\ x^-4)` `=x^-4`
Now
`Qe^(intPdx)=(x^5e^x) x^-4=xe^x`
Applying the formula: `ye^(intPdx)=intQe^(intPdx)dx+K` gives
`y\ x^(-4)=intxe^xdx+K`
This requires integration by parts, with
`u=x,` and `dv=e^xdx`
This gives us
`du=dx,` and `v=e^x`.
So
`y\ x^-4=xe^x-e^x+K`
Multiplying throughout by x4 gives us `y` as an explicit function of `x`:
`y=x^5e^x-x^4e^x+Kx^4`
Here is the solution graph for Example 5 (I've used K = 0.005).
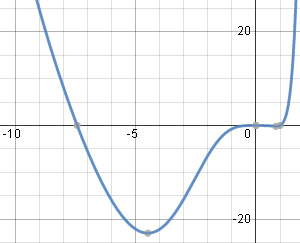
Typical solution graph using `K=0.005`.