3. Integrable Combinations
There are many differential equations where we cannot separate the variables, like we saw in the previous section.
However, we can possibly solve the DE if we use one of the following expressions to get the differential equation in a form that we can solve:
(1) `d(xy) = x dy + y dx`
(2) `d(x^2+ y^2) = 2(x dx + y dy)`
(3) `d(y/x)=(x dy-y dx)/x^2`
(4) `d(x/y)=(y dx-x dy)/y^2`
These differential forms are called integrable combinations. If we can transform our differential equation into one side of one of the above forms, then we can use the other side to solve the DE.
Where do these integrable combinations come from?
One way to think of the first expression above is as follows. Say x and y are both functions of t. If we have the product xy, then the derivative with respect to t of that product would be given by:
`d/(dt)(xy)=x(dy)/(dt)+y(dx)/(dt)`
(This is just the product rule that we learned ages ago.) Then we can multiply throughout by dt and we get the expression in (1) above, `d(xy) = x dy + y dx`.
We saw the second combination, `d(x^2+ y^2) = 2(x dx + y dy)`, back in implicit differentiation and related rates.
The third and fourth combinations are based on the Quotient Rule.
Example 1
Solve
(2y + x)dy + y dx = 0
Answer
First, we note that we cannot separate the variables such that the x expressions would be with dx only and the y expressions would be with dy only. So the DE is not separable.
So we aim to get the DE in one of the integrable combination forms. Rearranging, we have:
2y dy + (x dy + y dx) = 0
From the integrable combination (1) given above, the expression in brackets can be written as d(xy) and the differential equation is equivalent to:
2y dy + d(xy) = 0
Integrating gives us:
y2 + xy = K (General Solution)
CHECK
We obtained the solution y2 + xy = K. Is it correct?
Now
`d/dx y^2=2y dy/dx` (using Implicit Differentiation),
`d/dx xy=x dy/dx + y` (using product rule).
and `d/dx(k)=0`.
So putting this together gives the derivative of our answer as:
`2y(dy)/(dx)+x(dy)/(dx)+y=0`
On multiplying by dx throughout, we have:
2y dy + x dy + y dx = 0
which is the DE that we started with so we know our general solution is correct.
Here is the solution graph of our answer for Example 1 (I've used K = 25) . It is a hyperbola, with asymptotes y = −x, and the x-axis:
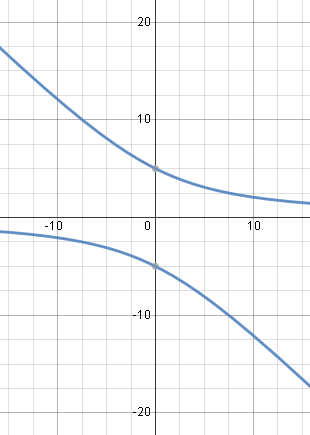
Solution using `K=25`.
Example 2
Solve
x dx = 9x2 dx − y dy
Answer
We recognise that we can get it in the form of the second expression at the top of this page.
We add y dy to both sides:
x dx + y dy = 9x2 dx
Now multiply both sides by 2:
2(x dx + y dy) = 18x2 dx
We see that the LHS is in the form of the second expression above. Now integrate both sides:
x2 + y2 = 6x3 + K
CHECK
Implicit differentiation gives us:
`2x + 2y(dy/dx) = 18x^2`Multiplying throughout by `dx/2` gives:
`x\ dx + y\ dy = 9x^2dx`
Subtracting y dy gives us our original DE
x dx = 9x2 dx − y dy
Here is the graph of our answer for Example 2 (using K = 9). It is an implicit function:
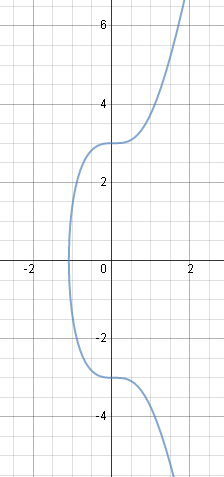
Solution using `K=2`.