IntMath Newsletter: Reuleaux triangles, hour of code

By Murray Bourne, 14 Dec 2015

14 Dec 2015

In this Newsletter:

1. Reuleaux triangles
2. Butterfly map of the world
3. Resource: Hour of code
4. Most popular stories in 2015
5. Math puzzles
6. Math movie: Rubik's cube and pianos
7. Final thought: head knowledge or skills?

1. Reuleaux triangles

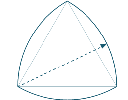Reuleaux triangles have a property similar to circles - they have constant diameter when rotated.

Reuleaux triangles

2. Butterfly map of the world

This article follows on from the one above. These maps are quite neat!

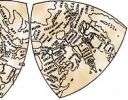The butterfly map of the world is based on Reuleaux triangles. This article explores some of the story behind this interesting map.

Butterfly map of the world

3. Hour of code

I'm a bit late for this, but no matter — it's available anytime.

Last week was "Hour of Code", one of the main events of Computer Science Education Week. The idea is to get students interested in programming by offering bite-sized tutorials in coding concepts, javascript and visual coding.

A lot of it appears to be aimed at younger kids, but there's lessons by Khan Academy, Codecademy and Google that could prove useful for older learners.

Should everyone learn code?

I attended a talk recently by a young professional programmer whose main point was that maybe not everyone needs to learn to code. There are many tools (like drag and drop types, and outsourcing) available to get things done without having to spend time actually coding.

This struck a chord with me because it's been my argument about (some parts of) mathematics for a long time now. That is, why do we make students spend hours solving equations, drawing graphs, finding derivatives and integrals, when most of it can be done using a computer algebra system more accurately, and in seconds?

Of course, "black box" solvers are dangerous if we don't know what we're doing (garbage in, garbage out, and if we don't understand what the computer gives us for an answer, then it's all quite useless).

Also, somebody needs to learn all the mathematics, otherwise who will create the useful tools in the future?

Similarly for computer programming. If everyone just uses tools without knowing what the tool is doing for them, then the overall skill level drops and eventually, no progress would be made.

For both fields, there should be a certain "cut off" point, where students know enough, and can be able to do enoough on paper, to appreciate what the machine can do for them, and what the machine's answer means. For example, in mathematics, it's silly getting students to solve 3x3 systems of equations on paper. If they can do 2x2 systems successfully, and can explain what to do with the answer, then good enough - let the computer do anything bigger.

An example from computing science is that anyone can build a Website now without any coding knowledge (see e.g. Google Sites, which promises "single click page creation" and "no HTML involved"). However, such tools always have limitations and it's always good to know how to tweak the code to get what you really want.

So what do you think - should all school students learn to code?

Coding credit?

On a related note, this news item has some interesting comments about the relative value of coding skills and mathematics:

University of California pressured to count computer science toward high school math requirement

Some students expect to get science credit for computer science qualifications. I agree with UC that it shouldn't happen, but it raises several issues about what skills students should really be gaining in school - especially schools in Silicon Valley.

4. Most popular stories in 2015

In case you missed any of them, here are the most popular IntMath Newsletter stories during the year, arranged by popularity (based on traffic).

Fundamental Theorem of Calculus applet

Is cube root the same as raising to power 1/3?

How to find the length of a spherical spiral

Pedigree collapse

Polar to Rectangular Online Calculator

Newton's Method Interactive Graph

Sampling to create mathematical function graphs

Work by a Variable Force using Integration

GraphFree

Is a 1x1 matrix a scalar?

Always popular this time of year:

The Twelve Days of Christmas - How Many Presents?

4. Math puzzles

The puzzle in the last IntMath Newsletter asked about the distance an ant walks on a coordinate plane.

Correct answers with explanation were given by: Rika (who nicely used the math input facility), Tomas, Nour (who correctly allowed for both arcs of the circle), Thomas, Saikrishna, and Darrell (who gave an exact answer).

As is often the case, the approaches used were quite varied.

New math puzzle

What is the ratio of the areas of the original equilateral triangle PQR (step 1) to the final Reuleaux triangle (step 3) in the Reuleaux triangle article, given that the segment through PQ in step 3 is 1.4 times the length of PQ?

You can leave your responses here.

5. Math movie: How to play a Rubik's Cube like a piano - Michael Staff

This movie explores the connections between Rubik's cube and the group theory concepts behind music.

Math movie: How to play a Rubik's Cube like a piano

6. Final thought: head knowledge or skills?

While conducting training for university teachers recently, I asked them to consider the following:

Employers don't care that much about what new graduates know. They care more about what employees can do with what they know, and their attitude towards doing it.

My point was it doesn't make sense to emphasize head knowledge (which we all forget as soon as we walk out of the examination), rather we should spend more time on developing skills and attitudes (which stay with us for much longer, and become more critical to our success in the future).

Do you agree with me?

I'd like to take this opportunity to wish everyone a Happy New Year, and a peaceful, happy and successful 2016.

The IntMath Newsletter will be back in mid-January.

Until next time, enjoy whatever you learn.

See the 14 Comments below.

Posted in Intmath Newsletters category - 14 Dec 2015 [Permalink]

14 Comments on “IntMath Newsletter: Reuleaux triangles, hour of code”

Murray says:
14 Dec 2015 at 3:21 pm [Comment permalink]
Please note the Puzzle responses are published just before publication of the next Newsletter.
Γιώργος Βαρελάς says:
14 Dec 2015 at 10:00 pm [Comment permalink]
(PQ) = a, new(PQ) = 1,4(PQ), 60/360 = 1/6, ratio =
{[a^2]*(3^0,5)/4]} / {3*π*[(1,4*α)^2]/6 - 2*[(1,4*a)^2]*[(3^0,5)]/4 + 3*π*[(0,4*a)^2]/6} = (3^0,5)/[2*(2,12*π - 1,96*(3^0,5)] = 0,2652
Adam C. Rinaldi says:
14 Dec 2015 at 10:30 pm [Comment permalink]
My question would be is what is being taught in schools. I have had experiences in both the US and Denmark where the computer system went down and the clerk could not help. Why? Because he/she could not figure what amount would be returned to me. When we can not do the basic things in math our world is doomed!
Phil Norman says:
14 Dec 2015 at 11:03 pm [Comment permalink]
In college I majored in physics minored in math until I was a Senior, then changed to business. I had a most excellent professor in business who really taught me "how to think and solve problems" more so than the ones in physics and math. On my entrance exam to become a pilot for the Air Force, I scored 99%. Today, I can't do any kind of calculus, differentiation, coding, etc. but I do know how to solve a variety of problems in business ( I never got my MBA or became a CPA, but because of my business professor's teaching....I can keep up with any in those fields.I agree with you that it is more important to know "how to think".

The one thing that did stick with me from all the physics courses that I took, was the value of approximation. I had always thought that physics was an exact science, only to find out that that is not the case. One case in particular from my experience occurred at a refinery in Nova Scotia. They had a particular vessel (only about a dozen of them in the world) that was operational and had an accumulation of hardened deposits that was limiting their operational efficiency. This situation was being discussed at a round table session of three other people plus myself. We knew the dimensions of the vessel, its internal configuration, % of operating efficiency, approximate density of material. We needed to know the weight of the deposit. By the use of approximation and doing some mental calculations within 30 seconds I come up with a figure. 10 minutes later, one of the plants engineers using a calculator come up with a figure that was within 1% of my estimation....then it took me another 5 minutes to explain to him how by approximating certain values that I was able to come up with that figure.
I can only thank my two college professors for teaching me how to use approximation and how to think....that has served me immensely in my careers.

I do enjoy reading your Math Newsletter, even though I don't understand most of it ...it refreshes my mind.
Bob Mrotek says:
14 Dec 2015 at 11:27 pm [Comment permalink]
"My point was it doesn't make sense to emphasize head knowledge (which we all forget as soon as we walk out of the examination), rather we should spend more time on developing skills and attitudes (which stay with us for much longer, and become more critical to our success in the future)."
Do you agree with me?

Yes, There are two requirements.
1.) To have knowledge in your head for comparative reference regarding rational thought.
2.) To understand the way the mind processes knowledge, reflex, habit, intuition, imagination, and emotion, etc.

Two places to start:
1.) John Dewey, "How We Think."
2.) William James, "Habit"

The decision between reflex or habit and rational thought is the difference between 0 and 1, not thinking, and thinking. With thinking there must be a decision.
Rusty Sinclair says:
15 Dec 2015 at 12:39 pm [Comment permalink]
I cast my vote for students needing to learn to code a little. I teach developmental math classes for Austin Community College and just finished teaching 17 students in a Basic Math Skills class. Yes, I told them that calculators could do things faster and more accurately, assuming that they input data correctly. However, things pop up with calculators like when you divide two whole numbers and get a decimal answer, how do you know what the remainder is. Maybe you need to know that for some reason. Also, students really need to understand how their calculators work (PEMDAS). I did not clue them in when we were calculating means until they calculated an answer and we discussed why the answer was so unreasonable; the calculator divided the last data entry before adding it to the total instead of getting the total first using the = button and then dividing by the number of data points. Yes, they were only using simple four-function calculators. These are just two examples and I always stress that my students need to know how to perform calculations on their own as well as estimate answers. Back to my original statement...coding gives students an idea of structure(s) and how things fit together in math, computer science, and all the other sciences. I try very hard to get them to understand the bigger picture and not just the discrete rules that we sometimes teach them because it is easier. And then we wonder why they cannot take what we taught them and apply it to the solving of problems.
cccccttttt says:
15 Dec 2015 at 12:44 pm [Comment permalink]
As a secondary math teacher it is my impression most students benefit far more from one year of computer science than from a year of calculus and a year of statistics combined.

But that aside,

1. As most students take calculus over again in college, it clearly is a waste for most students to do calculus at the high school level.

2. In grades 7/8 using a simple mesh and a composite line function one can find slopes and areas. To improve the approximation just refine the grid.

3. Even in theory I would argue for computer science.
IMO algorithms in coded form have more flexibility and power to express numerical relationships than the written traditional math statement.

4. Wolfram in "A New Kind of Science" expresses somewhat the same view.

Huff and Puff.

ct
Nour Hlwani says:
16 Dec 2015 at 6:53 am [Comment permalink]
1- Finding area of the equilateral triangle with side length = r ==>
${A}{\left({t}\right)}=\frac{{H}{e}{i}{g{h}}{t}.{B}{a}{s}{e}}{2}=\frac{{{r}{\sin{{\left(\frac{\pi}{3}\right)}}}{r}}}{2}=\frac{1}{4}{r}^{2}\sqrt{3}$

2- Finding area of the reuleux with pointed vertices.. a reuleux is constructed with 3 circles (each has radius r and origins are the three vertices) thus the area bounded by one circle and the triangle with opening angle $\frac{\pi}{3}$ can be written as ${A}{\left({c}\right)}=\frac{1}{2}{r}^{2}{\left(\frac{\pi}{3}-{\sin{{\left(\frac{\pi}{3}\right)}}}\right)}$ and the total area of the reuleux is then:
${A}{\left({r}\right)}={3}{A}{\left({c}\right)}+{A}{\left({t}\right)}=\frac{1}{2}{r}^{2}{\left(\pi-\sqrt{3}\right)}$

3- Finding the area of the extended reuleux.. with the hint that segment through PQ=1.4 PQ ==> radius of each circle =1.4r

Same method in -2- area between arc and triangle bounded by 0< $\theta$ <60 .. ${A}=\frac{1}{2}{{\left({1.4}{r}\right)}}^{2}\frac{\pi}{3}-{A}{\left({t}\right)}$
But we still need to find the spaces above the vertices .. we know that PQ=r and the whole segment=1.4r then the extended part would be r(1.4-1)=0.4r .. and the angles are opposed and we will have a tiny circle there that has radius 0.4r bounded by 0< $\theta$ ${A}{\left({s}\right)}=\frac{1}{2}\frac{\pi}{3}{{\left({0.4}{r}\right)}}^{2}=\frac{2}{75}\pi{r}^{2}$

And the whole extended reuleux area is then

${A}{\left({E}\right)}={3}{A}+{3}{A}{\left({s}\right)}+{A}{\left({t}\right)}=\frac{1}{2}{r}^{2}{\left(\frac{53}{25}\pi-\sqrt{3}\right)}$
Hamid.zandi says:
18 Dec 2015 at 2:09 am [Comment permalink]
Ans.
(Pi-3^0.5)/(2×pi-3^0.5)~.31
DON MILLLER says:
18 Dec 2015 at 3:12 pm [Comment permalink]
ans = 0.4831
triangle T area = sqr(3/4)
Pi =3.14159..
small= pi/2 - 2*T
large =(3pi/6)*(.04 +1.44-1)+small
small/large = 0.4831
Stephen says:
20 Dec 2015 at 12:11 pm [Comment permalink]
Puzzle solution:

(1) For the triangle PQR, let the side length be 1 unit.

Height of triangle PQR (from Pythagoras):

$\frac{\sqrt{3}}{2}$

Area of PQR:

$\frac{\sqrt{3}}{4}\approx{0.43301}$

(2) For the extended Reuleaux Triangle, the arc radius is 1.2 units and the included angle is $\frac{\pi}{3}$ .

There are 3 equal sized large sectors and 3 equal sized small sectors. I find area of one of each, then multiply by 3 to get total area.

The area of one of the large sectors is

$\text{Area}=\frac{{r}^{2}\theta}{2}=\frac{{{1.2}^{2}{\left(\pi\//{3}\right)}}}{2}={0.24}\pi$

If we just multiply by 3, we'll be counting triangle PQR 3 times, but we only want it once. So we take away 2 of them.

Total area of the large sectors is

${3}\times{0.24}\pi-{2}\times{0.43301}\approx{1.39592}$

The area of one of the small sectors is

$\text{Area}=\frac{{r}^{2}\theta}{2}=\frac{{{0.2}^{2}{\left(\pi\//{3}\right)}}}{2}={0.04}{\left(\frac{\pi}{6}\right)}\approx{0.02094}$

So the total area of the extended Reulueax Triangle is:

${1.39592}+{3}\times{0.02094}={1.45874}$

So the ratio of the area of triangle PQR to the area of the extended Reulueax Triangle is:

or
Murray says:
23 Dec 2015 at 4:44 pm [Comment permalink]
@Adam: I agree we still need to walk around with some basic knowledge (which has been truly mastered). But there is a cut off somewhere where it's better to leave the calculation for a computer to do.

@Phil: Yes, approximation is a key skill! This ensures we don't blindly accept our "black box" answers given by computers.

@Bob: I'm a big fan of Dewey's, and feel it's a shame his thoughts don't seem to pervade all educational institutions. I like your bit about the requirement to "understand the way the mind processes knowledge".

@Rusty: Blind use of calculators can be dangerous, as you said. I had a colleague who set exams with 2 portions - the first part students weren't allowed to use calculators (so they were encouraged to think) and in the last part (much shorter) they could use calculators. it sent a good message and probably is the way to go.

@cccccttttt: Here in Singapore, students are first introduced to calculus in the 4th year of junior school (around 16 years old), and develop it further from there. Probably students benefit most (when it comes to their overall life needs) by studying statistics, computer science and then calculus in that order... I agree with a lot of Wolfram's views, but there is a lot of commercial interest behind his statements.

Thanks everyone for your inputs!
anantha murthy says:
24 Dec 2015 at 11:43 pm [Comment permalink]
Dear sir, please explain to me the meaning of the following mathematical symbol as follows: there is an equals sign(=). On the top left & at the bottom right of this sign two dots(.) are placed. I am unable to find the explanation with the information source available with me . Please help me and thanks.
Murray says:
28 Dec 2015 at 4:31 pm [Comment permalink]
This is the closest I could find.

http://www.decodeunicode.org/en/u+2a77

Perhaps if you give a context (a screen shot or photo) showing the surrounding mathematics, it may help.

IntMath Newsletter: Reuleaux triangles, hour of code

1. Reuleaux triangles

2. Butterfly map of the world

3. Hour of code

Should everyone learn code?

Coding credit?

4. Most popular stories in 2015

4. Math puzzles

New math puzzle

5. Math movie: How to play a Rubik's Cube like a piano - Michael Staff

6. Final thought: head knowledge or skills?

14 Comments on “IntMath Newsletter: Reuleaux triangles, hour of code”

Leave a comment

Comment Preview

Tips

Categories

Most Commented

Recent Trackbacks

SquareCirclez is a "Top 100" Math Blog

IntMath Newsletter: Reuleaux triangles, hour of code

1. Reuleaux triangles

2. Butterfly map of the world

3. Hour of code

Should everyone learn code?

Coding credit?

4. Most popular stories in 2015

4. Math puzzles

New math puzzle

5. Math movie: How to play a Rubik's Cube like a piano - Michael Staff

6. Final thought: head knowledge or skills?

Related posts:

14 Comments on “IntMath Newsletter: Reuleaux triangles, hour of code”

Leave a comment

Comment Preview

Tips

Categories

Most Commented

Recent Trackbacks

SquareCirclez is a "Top 100" Math Blog

Want Better Math Grades?

Want Better Math Grades?

Tips, tricks, lessons, and tutoring to help reduce test anxiety and move to the top of the class.