7. Integration by Parts
by M. Bourne
Sometimes we meet an integration that is the product of 2 functions. We may be able to integrate such products by using Integration by Parts.
If u and v are functions of x, the product rule for differentiation that we met earlier gives us:
`d/(dx)(uv)=u(dv)/(dx)+v(du)/(dx)`
Rearranging, we have:
`u(dv)/(dx)=d/(dx)(uv)-v(du)/(dx)`
Integrating throughout with respect to x, we obtain the formula for integration by parts:
This formula allows us to turn a complicated integral into more simple ones. We must make sure we choose u and dv carefully.
NOTE: The function u is chosen so that `(du)/(dx)` is simpler than u.
Priorities for Choosing u
When you have a mix of functions in the expression to be integrated, use the following for your choice of `u`, in order.
1. Let `u = ln x`
2. Let `u = x^n`
3. Let `u = e^(nx)`
Example 1
`intx\ sin 2x\ dx`
Solution
We need to choose `u`. In this question we don't have any of the functions suggested in the "priorities" list above.
We could let `u = x` or `u = sin 2x`, but usually only one of them will work. In general, we choose the one that allows `(du)/(dx)` to be of a simpler form than u.
So for this example, we choose u = x and so `dv` will be the "rest" of the integral, dv = sin 2x dx.
We have `u = x` so `du = dx`.
Also `dv = sin 2x\ dx` and integrating gives:
`v=intsin 2x\ dx`
`=(-cos 2x)/2`
Substituting these 4 expressions into the integration by parts formula, we get (using color-coding so it's easier to see where things come from):
`int \color{green}{\underbrace{u}}\ \ \ \color{red}{\underbrace{dv}}\ \ ` ` =\ \ \color{green}{\underbrace{u}}\ \ \ \color{blue}{\underbrace{v}} \ \ -\ \ int \color{blue}{\underbrace{v}}\ \ \color{magenta}{\underbrace{du}}`
`int \color{green}{\fbox{:x:}}\ \color{red}{\fbox{:sin 2x dx:}} = \color{green}{\fbox{:x:}}\ \color{blue}{\fbox{:{-cos2x}/2:}} - int \color{blue}{\fbox{:{-cos2x}/2:}\ \color{magenta}{\fbox{:dx:}}`
` = (-xcos2x)/2 + 1/2 int cos2x dx`
` = (-xcos2x)/2 + 1/2 (sin2x)/2 +K`
` = (-xcos2x)/2 + (sin2x)/4 +K`
If the above is a little hard to follow (because of the line breaks), here it is again in a different format:
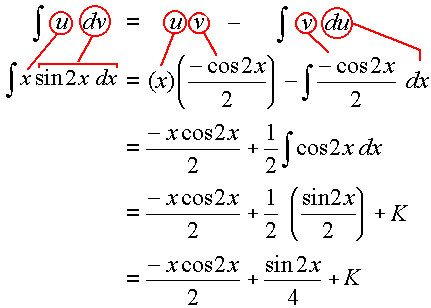
Example 2
`int x sqrt(x+1) dx`
Answer
`intxsqrt(x+1)\ dx`
We could let `u=x` or `u=sqrt(x+1)`.
Once again, we choose the one that allows `(du)/(dx)` to be of a simpler form than `u`, so we choose `u=x`.
Therefore `du = dx`. With this choice, `dv` must be the "rest" of the integral: `dv=sqrt(x+1)\ dx`.
`u = x` so `du=dx`.
`dv=sqrt(x+1)\ dx`, and integrating gives:
`v=intsqrt(x+1) dx`
`=int(x+1)^(1//2)dx`
`=2/3(x+1)^(3//2)`
Substituting into the integration by parts formula, we get:
`int \color{green}{\underbrace{u}}\ \ \ \color{red}{\underbrace{dv}}\ \ ` ` =\ \ \color{green}{\underbrace{u}}\ \ \ \color{blue}{\underbrace{v}} \ \ -\ \ int \color{blue}{\underbrace{v}}\ \ \color{magenta}{\underbrace{du}}`
`int \color{green}{\fbox{:x:}}\ \color{red}{\fbox{:sqrt(x+1) dx:}} = \color{green}{\fbox{:x:}}\ \color{blue}{\fbox{:2/3(x+1)^(3//2):}} ` `- int \color{blue}{\fbox{:2/3(x+1)^(3//2):}\ \color{magenta}{\fbox{:dx:}}`
` = (2x)/3(x+1)^(3//2) - 2/3 int (x+1)^{3//2}dx`
` = (2x)/3(x+1)^(3//2) ` `- 2/3(2/5) (x+1)^{5//2} +K`
` = (2x)/3(x+1)^(3//2)- 4/15(x+1)^{5//2} +K`
Once again, here it is again in a different format:
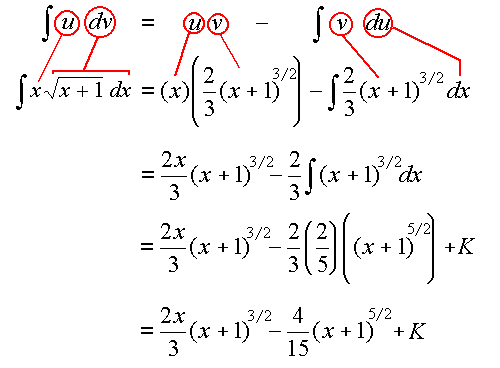
Example 3
`intx^2 ln 4x\ dx`
Answer
`intx^2ln\ 4x\ dx`
We could let `u=x^2` or `u=ln\ 4x`..
Considering the priorities given above, we choose `u = ln\ 4x` and so `dv` will be the rest of the expression to be integrated `dv = x^2\ dx`.
With `u=ln\ 4x`, we have `du=dx/x`.
Integrating `dv = x^2\ dx` gives:
`v=intx^2dx=x^3/3`
Substituting in the Integration by Parts formula, we get:
`int \color{green}{\underbrace{u}}\ \ \ \color{red}{\underbrace{dv}}\ \ ` ` =\ \ \color{green}{\underbrace{u}}\ \ \ \color{blue}{\underbrace{v}} \ \ -\ \ int \color{blue}{\underbrace{v}}\ \ \color{magenta}{\underbrace{du}}`
`int \color{green}{\fbox{:x^2:}}\ \color{red}{\fbox{:ln 4x dx:}} = \color{green}{\fbox{:ln 4x:}}\ \color{blue}{\fbox{:x^3/3:}} ` `- int \color{blue}{\fbox{:x^3/3:}\ \color{magenta}{\fbox{:dx/x:}}`
` = (x^3 ln 4x)/3 - 1/3 int x^2 dx`
` = (x^3 ln 4x)/3 ` `- 1/3 x^3/3 +K`
` = (x^3 ln 4x)/3 - x^3/9 +K`
Once again, here it is again in a different format:
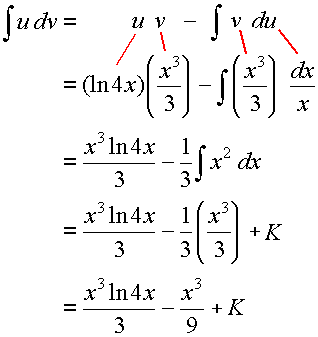
Example 4
`intx\ sec^2 x\ dx`
Answer
`int x\ sec^2 x\ dx`
We choose `u=x` (since it will give us a simpler `du`) and this gives us `du=dx`.
Then `dv` will be `dv=sec^2x\ dx` and integrating this gives `v=tan x`.
Substituting these into the Integration by Parts formula gives:
`int x\ sec^2 x\ dx =intu\ dv`
`=uv-intv\ du`
`=(x)(tan x)-int(tan x)dx`
`=x\ tan x-(-ln\ |cos x|)+K`
`=x\ tan x+ln\ |cos x|+K`
Example 5
`intx^2e^(-x)dx`
Answer
`intx^2 e^-x dx`
The 2nd and 3rd "priorities" for choosing `u` given earlier said:
2. Let `u = x^n`
3. Let `u = e^(nx)`
This questions has both a power of `x` and an exponential expression. But we choose `u=x^2` as it has a higher priority than the exponential. (You could try it the other way round, with `u=e^-x` to see for yourself why it doesn't work.)
So `u=x^2` and this gives `du=2x\ dx`.
That leaves `dv=e^-x\ dx` and integrating this gives us `v=-e^-x`.
We substitute these into the Integration by Parts formula to give:
`intx^2 e^-x dx =intu\ dv`
`=uv-intv\ du`
`=x^2(-e^-x)-int(-e^-x)(2x\ dx) `
`=-x^2e^-x+2intxe^-x dx `
Now, the integral we are left with cannot be found immediately. We need to perform integration by parts again, for this new integral.
This time we choose `u=x` giving `du=dx`.
Once again we will have `dv=e^-x\ dx` and integrating this gives us `v=-e^-x`.
Substituting into the integration by parts formula gives:
`int x e^-x dx =intu\ dv`
`=uv-intv\ du`
`=x(-e^-x)-int(-e^-x)dx`
`=-xe^-x+inte^-x dx`
`=-xe^-x-e^-x `
So putting this answer together with the answer for the first part, we have the final solution:
`intx^2e^-xdx =-x^2e^-x+2(-xe^-x-e^-x) `
`=-e^-x(x^2+2x+2)+K`
Example 6
`int ln x dx`
Answer
`int ln\ x\ dx`
Our priorities list above tells us to choose the logarithm expression for `u`. (of course, there's no other choice here. :-)
So with `u=ln\ x`, we have `du=dx/x`.
Then `dv` will simply be `dv=dx` and integrating this gives `v=x`.
Subsituting these into the Integration by Parts formula gives:
`int ln\ x\ dx=int u\ dv`
`=uv-intv\ du`
`=x\ ln\ x-intx(dx)/x`
`=x\ ln\ x-intdx`
`=x\ ln\ x-x+K`
Example 7
`intarcsin x dx`
Answer
Using integration by parts, we set:
`u=arcsin x`, giving `du=1/sqrt(1-x^2)dx`.
Then `dv=dx` and integrating gives us `v=x`.
We now use:
`intu\ dv=uv-intv\ du`
This gives us:
`int arcsin x\ dx` `=x\ arcsin x-intx/(sqrt(1-x^2))dx`
Now, for that remaining integral, we just use a substitution (I'll use `p` for the substitution since we are using `u` in this question already):
`p = 1 − x^2`
So `dp=-2x\ dx`
This will yield:
`intx/(sqrt(1-x^2))dx =-1/2int(dp)/sqrtp`
`=-1/2(2sqrtp)+K`
`=-sqrt(1-x^2)+K`
So our final answer is:
`int arcsin x\ dx =x\ arcsin x-(-sqrt(1-x^2))+K `
`= \x\ arcsin x+sqrt(1-x^2)+K`
This time we integrated an inverse trigonometric function (as opposed to the earlier type where we obtained inverse trigonometric functions in our answer). See Integration: Inverse Trigonometric Forms.
Alternate Method for Integration by Parts
Here's an alternative method for problems that can be done using Integration by Parts. You may find it easier to follow.