10. Reduction Formulae
by M. Bourne
You may have noticed in the Table of Integrals that some integrals are given in terms of a simpler integral. These require a few steps to find the final answer.
Reduction formulae are integrals involving some variable `n`, as well as the usual `x`. They are normally obtained from using integration by parts.
We use the notation `I_n` when writing reduction formulae.
Example 1
Given the reduction formula
`I_n=intsin^nx\ dx` `=-1/ncos x\ sin^(n-1)x+(n-1)/nI_(n-2),`
find `intsin^4x\ dx`.
Answer
Applying the reduction formula with `n = 4` gives:
`int sin^4x\ dx` `=-1/4cos x\ sin^3x+3/4I_2`
We now need to find `I_2=intsin^2x\ dx`, which corresponds to `n=2`.
Now, from our table of integrals,
`intsin^2xdx` `=x/2-1/2sin x\ cos x+K`
So putting it all together gives:
`intsin^4x\ dx`
`=-1/4cos x\ sin^3x` `+3/4[x/2-1/2sin x\ cos x+K]`
`=-1/4cos x\ sin^3x` `+3/8x` ` -3/8 cos x\ sin x+K^'`
`=3/8 x - 1/4 sin(2 x)` `+ 1/32 sin(4 x)+K^'` (afer some manipulation)
NOTE: We used `K` and `K^'` since the value of those constants is actually different.
For interest, here are the graphs of the function `y=sin^4 x` and its integral.
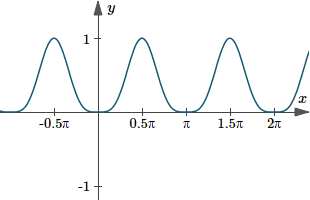
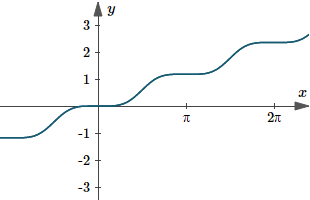
Graph of `y(x)=sin^4 x`, and its integral `y=3/8 x - 1/4 sin(2 x)+ 1/32 sin(4 x)` (I've used `K=0`).
Example 2
We are given that if
`I_n=inttan^nx\ dx`,
then `I_n=1/(n-1)tan^(n-1)x-I_(n-2).`
Find `inttan^3x\ dx`.
Answer
`inttan^3x\ dx=1/2tan^2x-I_1`
Now `I_1=inttan x\ dx` `=-ln\ |cos x|+K`
So `inttan^3x\ dx` `=1/2tan^2x+ln\ |cos x|+K`
Note: Often in this work there is more than one way to attack the question, so it is possible to get a correct answer, but in a different form. Using math software, like Scientific Notebook, you may get:
`inttan^3x\ dx` `=1/2tan^2x-1/2ln\ |1+tan^2x|`
Are the 2 answers the same?