6. Integration: Inverse Trigonometric Forms
by M. Bourne
Using our knowledge of the derivatives of inverse trigonometric identities that we learned earlier and by reversing those differentiation processes, we can obtain the following integrals, where `u` is a function of `x`, that is, `u=f(x)`.
`int(du)/sqrt(a^2-u^2)=sin^(-1)(u/a)+K`
`int(du)/(a^2+u^2)=1/atan^(-1)(u/a)+K`
NOTE: Your calculator has `sin^(-1)` and `tan^(-1)` buttons, but these create quite a bit of confusion because they are inverse functions, not reciprocals. We could also (better) write these formulas using `arcsin` and `arctan` as follows:
`int(du)/sqrt(a^2-u^2)=arcsin u/a+K`
`int(du)/(a^2+u^2)=1/a arctan u/a+K`
Example 1
Integrate: `int(dx)/sqrt(49-x^2`
Answer
Applying the formula, we have:
`int(dx)/(sqrt(49-x^2))=int(dx)/(sqrt((7)^2-x^2))`
`=sin^-1(x/7)+K`
We could also write this answer as:
`arcsin (x/7)+K`
This is the graph of the function we just integrated.
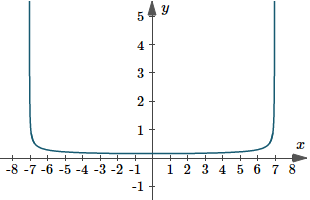
Graph of `y(x)=1/sqrt(49-x^2)`.
The next graph is a typical solution graph for the integral we just found, with `K=0`.
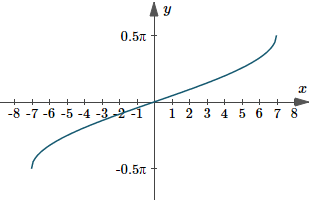
Graph of `y(x)=arcsin(x/7)`.
Example 2
Integrate: `int_0^1(2\ dx)/(sqrt(9-4x^2`
Answer
`int_0^1(2 dx)/(sqrt(9-4x^2`
Let `u=2x` then `du=2\ dx`.
Our integral becomes:
`int_0^1(2 dx)/(sqrt(9-4x^2))=int_(x=0)^(x=1)(du)/(sqrt((3)^2-u^2))`
`=[sin^-1(u/3)]_(x=0)^(x=1)`
`=[sin^-1 ((2x)/3)]_0^1`
`=[sin^-1 (2/3)-sin^-1 0]`
`=0.7297`
We could have done it in much fewer steps by leaving it in terms of "`u`", as follows:
`int_0^1(2 dx)/(sqrt(9-4x^2))=int_0^2(du)/(sqrt((3)^2-u^2))`
`=[sin^-1 (2/3)-sin^-1 0]`
`=0.7297`
Note the change in the limits when `dx` is changed to `du` during the integration.
This is because we let `u = 2x`.
Hence the limits for `x` of
`x = 0` and `x = 1`
have to be changed for `u` to
`u = 0` and `u = 2`.
Here is the graph of the integral we just found. It represents the area under the curve `y(x)=2/sqrt(9-4x^2)` from `0 < x < 1`.
Graph of `y(x)=2/sqrt(9-4x^2)`.
Example 3
Find the area bounded by the curve `y=1/(1+x^2)` and the lines x = 0, y = 0 and x = 2.
Answer
The curve `y=1/(1+x^2)` lies entirely above the `x`-axis for all values of `x`, so to find the area we can simply integrate. (If part of the curve was below the `x`-axis, we would need to split it into different portions and take absolute values.)
`"Area"=int_0^2(dx)/(1+x^2)`
`=[tan^-1x]_0^2`
`=[tan^-1 2-tan^-1 0]`
`=1.1071\ "units"^2`
This is the area we found just now.
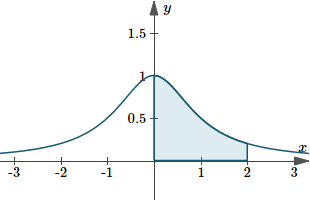
Graph of `y(x)=1/(1+x^2)` showing area between `0 < x < 2`.
Caution
There are a number of integrals of forms which look very similar to the above formulas but are actually different, e.g.
`int(dx)/(sqrt(x^2-1)),\ \ int(dx)/(sqrt(1+x^2)),` `\ \ int(dx)/(1-x^2),\ "etc."`
We will develop methods to solve these in a later section. (See Integration by Trigonometric Substitution.)
Exercises
Integrate each of the given functions:
1. `int(3\ dx)/(25+16x^2)`
Answer
We can write our integral as:
`int(3\ dx)/(25+16x^2)=3int(dx)/((5)^2+(4x)^2`
For the formula, we need:
`a = 5`; `u = 4x`; `du = 4\ dx`.Re-arranging that last expression gives: `(du)/4=dx`.
We are now ready to perform the integration.
`int(3\ dx)/(25+16x^2)=3/4int(du)/((5)^2+u^2)`
`=3/4xx1/5tan^-1 (u/5)+K`
`=3/20tan^-1 ((4x)/5)+K`
We could also write this answer as:
`3/20 arctan (4x)/5+K`
2. `int(2\ dx)/(x^2+8x+17)`
Answer
`int(2 dx)/(x^2+8x+17`
Now
`x^2+8x+17=(x^2+8x+16)+1`
`=(x+4)^2+1`
So if we let `u = x + 4`, then `du = dx` and we have:
`int(2\ dx)/(x^2+8x+17)=2int(du)/(u^2+1)`
`=2\ tan^-1u+K`
`=2\ tan^-1(x+4)+K`
Of course, we could also write this answer as
`2\ arctan(x+4)+K`
3. `int(dx)/(sqrt(2x-x^2)`
Answer
`int(dx)/(sqrt(2x-x^2)`
This is not in the form of either of our new formulas, but we can do some juggling to get it into a useful form.
First, we recognise that
`2x-x^2=-(x^2-2x)`
We now add `1` at the front, then compensate for it inside the bracket:
`=1-(x^2-2x+1)`
`=1-(x-1)^2`
With `a = 1`; `u = x - 1`, and `du = dx`, our integral becomes:
`int(dx)/(sqrt(2x-x^2))=int(du)/(sqrt(1-u^2))`
`=arcsin u+K`
`=arcsin(x-1)+K`
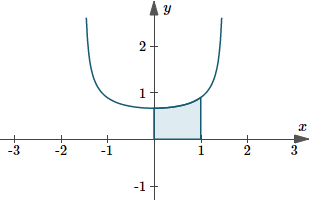
4. Find the area bounded by the curve `ysqrt(4-x^2)=1` and the lines `x = 0`, `y = 0` and `x = 1`.
Answer
The curve's function can be written:
`y=1/sqrt(4-x^2)`
This curve is completely above the `x`-axis for all values of `x` such that `-2 < x < 2`, as we can see in the graph below. (It's not defined for any other values of `x`).
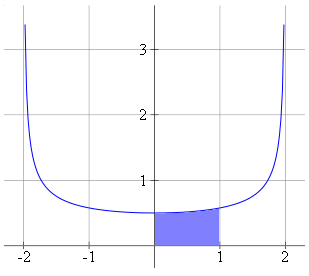
So to find the required area (the shaded portion) we can simply integrate.
`A=int_0^1 1/(sqrt(4-x^2))dx`
`=[arcsin(x/2)]_0^1`
`=pi/6-0`
`=0.5236`