1a. The Unit Step Function (Heaviside Function)
In engineering applications, we frequently encounter functions whose values change abruptly at specified values of time t. One common example is when a voltage is switched on or off in an electrical circuit at a specified value of time t.
The value of t = 0 is usually taken as a convenient time to switch on or off the given voltage.
The switching process can be described mathematically by the function called the Unit Step Function (otherwise known as the Heaviside function after Oliver Heaviside).
The Unit Step Function
Definition: The unit step function, `u(t)`, is defined as
`u(t)={: {(0, t < 0), (1, t > 0) :}`
That is, u is a function of time t, and u has value zero when time is negative (before we flip the switch); and value one when time is positive (from when we flip the switch).
Graph of `f(t)=u(t)`, the unit step function.
Value at t = 0?
In some text books you will see the unit step function defined as having value 1 at t = 0, as follows:
`u(t)={: {(0, t < 0), (1, t >= 0) :}`
We would indicate the discontinuity on our graph like this:
Graph of `f(t)=u(t)`, the unit step function, with `f(0) = 1`.
Also, sometimes you'll see the value given as `f(0) = 0.5`.
In this work, it doesn't make a great deal of difference to our calculations, so we'll continue to use the first interpretation, and draw our graphs accordingly.
Shifted Unit Step Function
In many circuits, waveforms are applied at specified intervals other than `t=0`. Such a function may be described using the shifted (aka delayed) unit step function.
Definition of Shifted Unit Step Function
A function which has value `0` up to the time `t = a` and thereafter has value `1`, is written:
`u(t-a)={{: (0, if, t < a), (1, if, t > a) :}`
Example 1 - Shifted Unit Step Function
`f(t) = u(t − 3)`
The equation means f(t) has value of `0` when `t < 3` and `1` when `t > 3`.
The sketch of the waveform is as follows:
Graph of `f(t)=u(t-3)`, a shifted unit step function.
Rectangular Pulse
A common situation in a circuit is for a voltage to be applied at a particular time (say t = a) and removed later, at t = b (say). We write such a situation using unit step functions as:
`V(t) = u(t − a) − u(t − b)`
This voltage has strength `1`, duration `(b − a)`.
Example 2 - Rectangular Pulse
The graph of `V(t) = u(t − 1.2) − u(t − 3.8)` is as follows. Here, the duration is `3.8 − 1.2 = 2.6`.
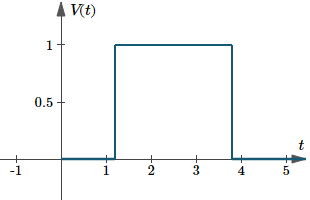
Graph of `V(t)=u(t−1.2)−u(t−3.8)`, an example of a rectangular pulse.
Exercises
Need Graph Paper?
Write the following functions in terms of unit step function(s). Sketch each waveform.
(a) A 12-V source is switched on at t = 4 s.
Answer
Since the voltage is turned on at t = 4, we need to use u(t − 4). We multiply by 12 since that is the voltage.
We write the function as follows:
`V(t)=12·u(t-4)`.
Here's the graph:
Graph of `V(t)=12·u(t-4)`, a shifted step function.
(b) `V(t)={{: (1, 0 < t < a),(0, t > a) :}`
(Assume a > 0.)
Answer
In words, the voltage has value `1` up until time `t = a`. Then it is turned off.
We have a "rectangular pulse" situation and need to use this formula:
`V(t) = u(t − a) − u(t − b)`
In our example, the pulse starts at `t = 0`, so we use `u(t)`, and finishes at `t = a`, so we use `u(t − a)`.
So the required function is:
`V(t)=1·[u(t)-u(t-a)]` `=u(t)-u(t-a)`
Graph of `V(t)=u(t)-u(t-a)`, a shifted unit step function.
(c) One cycle of a square wave, `f(0) = 4`, amplitude = `4`, period = `2` seconds.
Answer
`f(0) = 4` means we start at value `4`.
If the whole wave has period `2`, and it is a square wave, then it means for half of the time, the value is (positive) `4` and the other half it is `-4`.
So for the first second, it has value `4`, for the second second, the function value is `-4`.
We write this, using the "rectangular pulse" formula from before:
`f(t) = 4·{u(t) − u(t − 1)}` `-4·{u(t-1) − u(t − 2)}`
`=4·u(t)-8·u(t-1)+4·u(t-2)`
The graph of this first cycle is:
Graph of `f(t)=4·u(t)-8·u(t-1)+4·u(t-2)`, a square wave.
(d) The unit Ramp function (i.e.`f(t) = t` for `t > 0`)
Answer
The unit ramp function has slope `1` [so the function is simply `V(t) = t`], starting from `t = 0` [so we need to multiply by `u(t)`], and passes through `(0, 0)`.
So the voltage function is given by:
`V(t) = t · u(t)`
The graph of the function is:
Graph of `V(t)=t · u(t)`, the unit ramp function.
(e) One cycle of a sawtooth waveform (i.e. `f(t)=a/b t` for `0 < t < b`. Assume `a > 0`.)
Answer
Our graph starts at `t = 0` and has slope `a / b`. It finishes at `t = b`.
So our function will be:
`f(t)=a/b t · {u(t)-u(t-b)}`
The graph of our function:
Graph of `f(t)=a/b t · {u(t)-u(t-b)}`, a sawtooth waveform.
(f) `V(t)={ {: (0,t < 3), (2t+8,3 < t < 5), (0,t > 5) :}`
Answer
In this example, our function is `V(t) = 2t + 8` which has slope `2` and `V`-intercept `8`.
The signal is only turned on between `t = 3` and `t = 5`. The rest of the time it is off.
So our voltage function will be:
`V(t) ` `= (2t+8) ·{u(t − 3)− u(t − 5)}`
The graph is as follows:
Graph of `V(t) = (2t+8) ·{u(t − 3)− u(t − 5)}`. The dashed line is `V(t) = 2t + 8`.
