5. Solving Trigonometric Equations
by M. Bourne
Trigonometric equations can be solved using the algebraic methods and trigonometric identities and values discussed in earlier sections. You may wish to go back and have a look at Trigonometric Functions of Any Angle, where we see the background to the following solutions.
A painless way to solve these is using a graph. Where the graph cuts the x-axis, that's where you'll find your solutions (the x-values that "work"). Graphs also help you to understand why sometimes there is one answer, and sometimes many answers. I use Scientific Notebook or similar math software to graph the functions for me.
You can use this Online Graphing Calculator to solve the following equations (or check your solutions) .
Example 1
Solve the equation 2 cos θ − 1 = 0 for 0 ≤ θ < 2π.
Answer
Rearranging the above equation, we get:
`cos theta=1/2`
We know the following :
Since
`cos (pi/3) = 1/2`
and `cos θ` is positive in the first and fourth quadrants, we have:
`theta=pi/3`
or
`theta=2pi-pi/3=(5pi)/3`
So `theta=pi/3` or `theta=(5pi)/3`
Example 2
Revision Tip
Getting lost in this section? See the background at Trigonometric Functions of Any Angle
Graphically solve the equation
2 cos2x − sin x − 1 = 0
such that 0 ≤ θ < 2π.
Answer
Using graphing software, we draw the curve of y = 2 cos2x − sin x − 1 in the region 0 ≤ θ < 2π. Wherever the curve cuts the x-axis will be the solution for our equation.
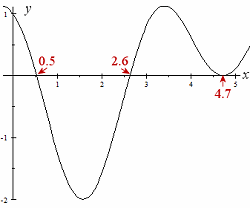
We see from the graph that the solutions are approximately:
x = 0.5
x = 2.6
x = 4.7
For more accurate solutions, we would just zoom in on the graph.
In this next graph, I have zoomed in to the second root (the one near x = 2.6). We can see that this root is x = 2.618 correct to 3 decimal places.
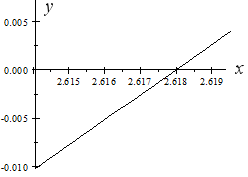
We could continue to zoom in as close as we like to get the accuracy that we require.
Solving Equations Involving Multiples of θ
Example 3
Solve the equation sin 2θ = 0.8 for 0 ≤ θ < 2π.
Answer
If the problem involved θ only, we would expect 2 solutions; one in the first quadrant and one in the second quadrant.
But here our problem involves `2θ`, so we have to double the domain (θ values) to account for all possible solutions.
We proceed as follows:
We solve
`sin 2θ = 0.8` for 0 ≤ 2θ < 4π.
The reference angle is
`α = arcsin 0.8 = 0.9273`
So the values for 2θ will be in quadrants I, II, V, VI.
2θ = 0.9273, or π − 0.9273, or 2π + 0.9273, or 3π − 0.9273
That is
`2θ = 0.9273, 2.2143, 7.2105, 8.4975`
But we need values for θ, not 2θ, so we divide throughout by 2:
`θ = 0.4637, 1.1072, 3.6053, 4.2488`
Are our answers correct? As usual, we will check by graphing the original expression:
We can see from the graph that our 4 values are reasonable, since these are the only 4 values that satisfy `sin 2θ = 0.8`.
Note: We can always check our solutions with calculator, but it is easy to "miss out" on some of the required values if we only use calculator.
Example 4
Solve the equation
`cos^2theta=1/16`
for 0 ≤ θ < 2π.
Answer
Solving for cos θ gives us:
`cos theta=+-1/4`
If `cos alpha=1/4`, then the reference angle is α = 1.3181.
So for `cos theta=1/4`, we have θ in the first and 4th quadrants. So
`θ = 1.3181 or 4.9651`
For `cos theta=-1/4`, we have θ in the 2nd and 3rd quadrants. So
`θ = 1.8235 or 4.4597`
So ` θ= 1.3181, 1.8235,` ` 4.4597` ` or 4.9651` radians.
We can see from the graph of `y=cos^2theta-1/16` that our answer is correct:
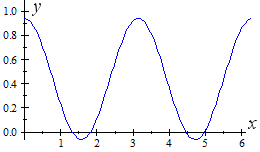
Example 5
Solve the equation
6 sin2θ − sin θ − 1 = 0
for 0 ≤ θ < 2π.
Answer
Factoring the LHS:
`6 sin^2θ − sin θ − 1 = 0`
`(2 sin θ − 1)(3 sin θ + 1) = 0`
So either
`2 sin θ − 1 = 0`
`sin θ = 1/2`
θ will be in 1st and 2nd quadrants.
`θ = 0.52360, 2.6180` (that is, `pi/6` or `(5pi)/6`)
OR
`3 sin θ + 1 = 0`
`sin θ = − 1/3`
θ will be in 3rd and 4th quadrants.
`θ = 3. 4814, 5. 9433`
Checking our solution on a graph:
So `θ = 0.52360, 2.6180, 3. 4814, 5. 9433`
Example 6
Solve the equation
`cos{:x/2:}=1+cos\ x`
for 0 ≤ θ < 2π.
Answer
Earlier we learned that `cos(x/2)=+-sqrt((1+cos x)/2)`, so we have:
`+-sqrt((1+cos x)/2)= 1 + cos x`
Squaring both sides gives:
`(1+cos x)/2=(1+cos x)^2`
`(1+cos x)/2=1+2\ cos x+cos^2x`
`1+cos x=2+4\ cos x+2\ cos^2x`
So we have:
`2\ cos^2 \ x + 3\ cos x + 1 = 0``(2\ co\s x + 1)(cos x + 1) = 0`
Solving, we get
`cos x = − 0.5` or `cos x = − 1`
Now `cos x=-1/2` gives `x=(2pi)/3,(4pi)/3`.
However, on checking in the original equation, we note that
`"LHS"=cos((4pi)/3xx1/2)` `=cos((2pi)/3)` `=-1/2`
but
`"RHS"=1+cos (4pi)/3=+1/2`
So the only solution for this part is `x=(2pi)/3.`
Also, `cos x=-1` gives `x = pi`.
So the solutions for the equation are `x=(2pi)/3or pi.`
A check of the graph of `y=cos x/2-1-cos x` confirms these results:
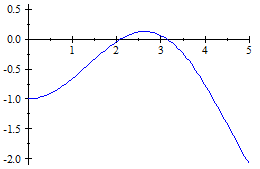
(2π/3 ≈ 2.0944 and π ≈ 3.14).
Example 7
Solve the equation
tan 2θ − cot 2θ = 0
for 0 ≤ θ < 2π.
Answer
`cot 2theta= 1/(tan 2 theta)`, so we have:
`tan 2 theta-1/(tan 2 theta)=0`
`tan^2 2θ = 1`
`tan 2θ = ± 1`
Since `0 ≤ θ < 2π`, we need to consider values of `2theta` such that `0 ≤ 2θ < 4π`. Hence, solving the above equation, we have:
`2 theta=pi/4,(3pi)/4,(5pi)/4(7pi)/4,` `(9pi)/4,(11pi)/4,` `(13pi)/4,(15pi)/4`
Dividing throughout by 2 gives us the full set of solutions in the required domain, `0 <= theta <2pi`:
`theta=pi/8,(3pi)/8,` `(5pi)/8,(7pi)/8,` `(9pi)/8,(11pi)/8,` `(13pi)/8,(15pi)/8`
Exercises
Note 1: "Analytically" means use the methods and formulas from previous sections. It means don't just use a graph to solve it.
Note 2: However, I always use a graph to check my analytical work. I can see immediately if some error has occurred. I encourage you to do the same!
1. Solve the trigonometric equation analytically
4 tan x − sec2 x = 0 (for 0 ≤ x < 2π)
Answer
`4\ tan x− sec^2x= 0`
Writing this in terms of `sin x` and `cos x` only:
`4(sin x)/(cos x)-1/(cos^2x)=0`
Multiplying throughout by `cos x`:
`4\ sin x\ cos x=1`
Dividing both sides by 2:
`2\ sin x\ cos x=1/2`
Recognizing the LHS is `sin 2x`, from before:
`sin 2x,=0.5`
In 0 ≤ x < 2π, we need to find values of 2x such that 0 ≤ 2x < 4π. (Twice the original domain.)
So the values for `2x` are:
`2x=pi/6,(5pi)/6,(13pi)/6,(17pi)/6`
Dividing throughout by 2 gives our required values for `x`:
`x=pi/12,(5pi)/12,(13pi)/12,(17pi)/12`
or, in decimal form:
`x = 0.2618, 1.309, 3.403, 4.451`
2. Solve the trigonometric equation analytically for 0 ≤ x < 2π:
sin 2x cos x − cos 2x sin x = 0
Answer
We recognise the left hand side to be in the form:
`sin(a − b) =` ` sin a cos b − cos a sin b,`
where `a = 2x` and `b =x`.
So
`sin 2x\ cos x − cos 2x\ sin x`
`= sin(2x − x)`
`= sin x`
Now, we know the solutions of `sin x = 0` to be:
`x = 0, π`.
[Why?]
Need Graph Paper?
3. Solve the given trigonometric equation analytically and by graphical method (for 0 ≤ x < 2π):
sin 4x − cos 2x = 0
Answer
sin 4x − cos 2x = 0
2sin 2x cos 2x − cos 2x = 0
Factoring gives:
cos 2x (2 sin 2x − 1) = 0
EITHER
`cos 2x= 0`
`2x=pi/2,(3pi)/2,(5pi)/2,(7pi)/2`
`x=pi/4,(3pi)/4,(5pi)/4,(7pi)/4`
OR
`sin 2x= 1/2`
`2x=pi/6,(5pi)/6,(13pi)/6,(17pi)/6`
`x=pi/12,(5pi)/12,(13pi)/12,(17pi)/12`
Or, in decimal form:
`x= 0.26, 0.79, ` `1.31, 2.36, ` `3.40, 3.93, ` `4.45, 5.50.`
The graph of `y = sin 4x− cos 2x` is as follows. We can see from where the graph cuts the x-axis that our answers are reasonable.