9. Impedance and Phase Angle
Don't miss...
Explore impedance, current and voltage in an RLC circuit in the applet later on this page.
Impedance
The impedance of a circuit is the total effective resistance to the flow of current by a combination of the elements of the circuit.
Symbol: Z
Units: `Ω`
The total voltage across all 3 elements (resistors, capacitors and inductors) is written
VRLC
To find this total voltage, we cannot just add the voltages VR, VL and VC.
Because VL and VC are considered to be imaginary quantities, we have:
Impedance VRLC = IZ
So `Z = R + j(X_L− X_C)`
Now, the magnitude (size, or absolute value) of Z is given by:
`|Z|=sqrt(R^2+(X_L-X_C)^2`
Phase angle
`tan\ theta=(X_L-X_C)/R`
Angle θ represents the phase angle between the current and the voltage.
Compare this to the Phase Angle that we met earlier in Graphs of y = a sin(bx + c).
Example 1
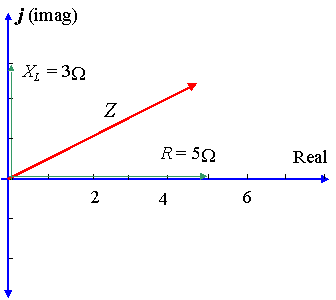
A circuit has a resistance of `5\ Ω` in series with a reactance across an inductor of `3\ Ω`. Represent the impedance by a complex number, in polar form.
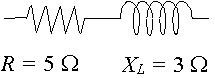
Answer
In this case, `X_L= 3\ Ω` and `X_C= 0` so `X_L- X_C= 3\ Ω`.
So in rectangular form, the impedance is written:
`Z = 5 + 3j\ Ω`
Using calculator, the magnitude of Z is given by: `5.83`, and the angle `θ` (the phase difference) is given by: `30.96^@`.
So the voltage leads the current by `30.96^@`, as shown in the diagram.
Presenting Z as a complex number (in polar form), we have:
`Z = 5.83 ∠ 30.96^@\ Ω`.
Example 2(a)
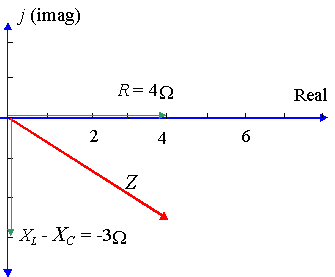
A particular ac circuit has a resistor of `4\ Ω`, a reactance across an inductor of `8\ Ω` and a reactance across a capacitor of `11\ Ω`. Express the impedance of the circuit as a complex number in polar form.
Answer
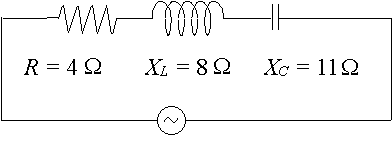
In this case, we have: `X_L- X_C= 8 - 11 = -3\ Ω`
So `Z = 4 - 3j\ Ω` in rectangular form.
Now to express it in polar form:
Using calculator, we find `r = 5` and ` θ = -36.87^@`.
[NOTE: We usually express the phase angle (when voltage lags the current) using a negative value, rather than the equivalent positive value `323.13^@`.]
So `Z = 5 ∠ -36.87^@\ Ω`
Interactive RLC graph
Below is an interactive graph to play with (it's not a static image). You can explore the effect of a resistor, capacitor and inductor on total impedance in an AC circuit.
Activities for this Interactive
- First, just play with the sliders. You can:
Drag the top slider left or right to vary the impedance due to the resistor, `R`,
Drag the XL slider up or down to vary the impedance due to the inductor, `X_L`, and
Drag the XC slider up or down to vary the impedance due to the capacitor, `X_C`. - Observe the effects of different impedances on the values of XL − XC and Z.
- Observe the effects of different impedances on θ, the angle the red "result" line makes with the horizontal (in radians).
- Consider the graphs of voltage and current in the interactive. Observe the amount of lag or lead as you change the sliders.
- What have you learned from playing with this interactive?
Copyright www.intmath.com
Example 2(b)
Referring to Example 2 (a) above, suppose we have a current of 10 A in the circuit. Find the magnitude of the voltage across
i) the resistor (VR)
ii) the inductor (VL)
iii) the capacitor (VC)
iv) the combination (VRLC)
Answer
i) | VR | = | IR | = 10 × 4 = 40 V
ii) | VL | = | IXL | = 10 × 8 = 80 V
iii) | VC | = | IXC | = 10 × 11 = 110 V
iv) | VRLC | = | IZ | = 10 × 5 = 50 V