7. Powers and Roots of Complex Numbers
by M. Bourne
Consider the following example, which follows from basic algebra:
(5e3j)2 = 25e6j
We can generalise this example as follows:
(rejθ)n = rnejnθ
The above expression, written in polar form, leads us to DeMoivre's Theorem.
DeMoivre's Theorem
[r(cos θ + j sin θ)]n = rn(cos nθ + j sin nθ)
where `j=sqrt(-1)`. Equivalently,
(r∠θ)n = rn ∠nθ
Challenge
I'm going to challenge you here...
I have never been able to find an electronics or electrical engineer that's even heard of DeMoivre's Theorem. Certainly, any engineers I've asked don't know how it is applied in 'real life'.
I've always felt that while this is a nice piece of mathematics, it is rather useless.. :-)
Here are some responses I've had to my challenge:
Some possibilities
I received this reply to my challenge from user Richard Reddy:
Much of what you're doing with complex exponentials is an extension of DeMoivre's Theorem. In general, the theorem is of practical value in transforming equations so they can be worked more easily. Often, what you see in EE are the solutions to problems in physics. There was a time, before computers, when it might take 6 months to do a tensor problem by hand. DeMoivre's theorem is a time-saving identity, easier to apply than equivalent trigonometric identities.
I like your site.
And this came in from Russell Davies:
I'm an electronics engineer. In terms of practical application, I've seen DeMoivre's Theorem used in digital signal processing and the design of quadrature modulators/demodulators.
Reader Andy added:
DeMoivre's Theorem can be used to find the secondary coefficient Z0 (impedance in ohms) of a transmission line, given the initial primary constants R, L, C and G. (resistance, inductance, capacitance and conductance) using the equation
`Z_0=sqrt((R+jomegaL)/(G+jomegaC))`,
where '`omega`' is the angular frequency of the supply in radians per second. In this case, the power 'n' is a half because of the square root and the terms inside the square root can be simplified to a complex number in polar form.
Reader David from IEEE responded with:
De Moivre's theorem is fundamental to digital signal processing and also finds indirect use in compensating non-linearity in analog-to-digital and digital-to-analog conversion.
After those responses, I'm becoming more convinced it's worth it for electrical engineers to learn deMoivre's Theorem. Please let me know if there are any other applications.
Example 1
Find (1 − 2j)6
Answer
First, we express `1 - 2j` in polar form:
`sqrt(1^2 + (-2)^2)=sqrt(5)`, and
`arctan((-2)/1) =296.6^"o"`
So
`1-2j=sqrt5\ /_ \ 296.6^text(o)`
Then
`(1-2j)^6=(sqrt5)^6/_ \ [6xx296.6^text(o)]`
`=125\ /_ \ [1779.3903^text(o)]`
`=125\ /_ \ [339.39^text(o)]`
(The last line is true because `360° × 4 = 1440°`, and we substract this from `1779.39°`.)
In rectangular form,
x = 125 cos 339.39o = 117
y = 125 sin 339.39o = -44
So (1 - 2j)6= 117 - 44j
Complex Roots
If an = x + yj then we expect n complex roots for a.
Example 2
If a5 = 7 + 5j, then we expect `5` complex roots for a.
Spacing of n-th roots
In general, if we are looking for the n-th roots of an equation involving complex numbers, the roots will be `360^"o"/n` apart. That is,
2 roots will be `180°` apart
3 roots will be `120°` apart
4 roots will be `90°` apart
5 roots will be `72°` apart etc.
Example 3
Find the two square roots of `-5 + 12j`.
Answer
For the first root, we need to find `sqrt(-5+12j`.
This is the same as (-5 + 12j)1/2.
We express −5 + 12j in polar form:
`r=sqrt((-5)^2+12^2=13`
For the angle:
`alpha=tan^-1(y/x)`
`=tan^-1(12/5)~~67.38^text(o)`
The complex number −5 + 12j is in the second quadrant, so
θ = 180° − 67.38 = 112.62°
So
`−5 + 12j = 13 ∠ 112.62°`
Using DeMoivre's Theorem:
`(r ∠ θ)^n=(r^n∠ nθ)`,
we have:
`(-5+12j)^(1"/"2)`
`=13^(1"/"2)/_(1/2xx112.62^@)`
`=3.61/_56.31^@`
This is the first square root. In rectangular form,
x = 3.61 cos56.31° = 2
y = 3.61 sin56.31° = 3
So the first root is 2 + 3j.
CHECK: (2 + 3j)2 = 4 + 12j - 9 = -5 + 12j [Checks OK]
To obtain the other square root, we apply the fact that if we need to find n roots they will be `360^text(o)/n` apart.
In this case, `n = 2`, so our roots are `180°` apart.
Adding `180°` to our first root, we have:
x = 3.61 cos(56.31° + 180°) = 3.61 cos(236.31°) = -2
y = 3.61 sin(56.31° + 180°) = 3.61 sin(236.31°) = -3
So our second root is `-2 - 3j`.
So the two square roots of `-5 - 12j` are `2 + 3j` and `-2 - 3j`.
Exercises:
1. Evaluate `(2 ∠ 135^@)^8`
Answer
`(2 ∠ 135^@)^8= (2)^8 ∠ (135^@ × 8)`
`= 256 ∠ 1080^@`
`= 256`
2. Find: (−2 + 3j)5
Answer
(−2 + 3j)5
= (3.60555 ∠ 123.69007°)5 (converting to polar form)
= (3.60555)5 ∠ (123.69007° × 5) (applying deMoivre's Theorem)
= 609.33709 ∠ 618.45035°
= −121.99966 − 596.99897j (converting back to rectangular form)
= −122.0 − 597.0j (correct to 1 decimal place)
For comparison, the exact answer (from multiplying out the brackets in the original question) is
−122 − 597j
[Note: In the above answer I have kept the full number of decimal places in the calculator throughout to ensure best accuracy, but I'm only displaying the numbers correct to 5 decimal places until the last line.]
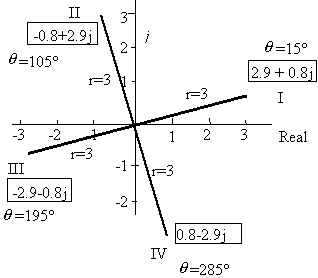
3. (i) Find the first 2 fourth roots of 81(cos 60o + j sin 60o)
(ii) Then sketch all fourth roots of 81(cos 60o + j sin 60o) showing relevant values of r and θ.
Answer
Part (i)
There are 4 roots, so they will be `θ = 90^@` apart.
I First root:
`81^(1"/"4)[cos\ ( 60^text(o))/4+j\ sin\ (60^text(o))/4]`
`= 3(cos\ 15^"o" + j\ sin\ 15^"o")`
` = 2.90 + 0.78j`
II Second root:
Add `90°` to the first root:
3(cos(15o + 90o) + j sin(15o + 90o))
= 3(cos105o + j sin 105o)
= -0.78 + 2.90j
So the first 2 fourth roots of 81(cos 60o + j sin 60o) are:
`2.90 + 0.78j` and `-0.78 + 2.90j`
Part (ii)
In each case, r = 811/4 = 3
4. At the beginning of this section, we expected 3 roots for
`x^3= 8`.
Find the roots and sketch them.
Answer
In polar form, 8 = 8(cos 0o + j sin 0o).
There are 3 roots, so they will be `θ = 120°` apart.
Using DeMoivre's Theorem:
an = rn(cos nθ + j sin nθ),
First root:
`8^(1"/"3)=8^(1"/"3)(cos\ 0^text(o)/3+j\ sin\ 0^text(o)/3)`
`=2(cos\ 0^text(o)+j\ sin0^text(o))`
`=2`
Second root:
Add `120°` to the first root:
81/3(cos 120o + j sin 120o) = −1 + 1.732j
Third root:
Add `120°` to the second root:
81/3(cos 240o + j sin 240o) = −1 − 1.732j
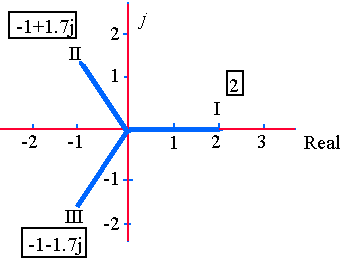
So the 3 cube roots of `8` are:
To see if the roots are correct, raise each one to power `3` and multiply them out.