8. An Application of Complex Numbers: AC Circuits

by M. Bourne

Before we see how complex numbers can help us to analyse and design AC circuits, we first need to define some terms.

Definitions

Resistance

Symbol: R

Units: Ω (ohms)

A resistor is any part of a circuit that obstructs the flow of current.

Capacitance

Symbol: C

Units: `"F"` (farads)

A capacitor consists of 2 non-connected plates:

Inductance

Symbol: L

Units: `"H"` (henrys)

An inductor is coil of wire in which current is induced.

Current: I (in amperes)

Voltage: V (in volts).

Ohm's Law: `V = IR`

Reactance

Reactance is the effective resistance of any part of the circuit. This could be from an inductor or a capacitor. See more in the next section Impedance and Phase Angle.

Symbol: X

Voltage in alternating current circuits

• The voltage across a resistance is in phase with the current .

• The voltage across a capacitor lags the current by `90^@`.

• The voltage across an inductance leads the current by `90^@`

For voltage: V = IX

The voltage across a resistor with resistance R:

V_R = IR

The voltage across a capacitor with reactance X_C (voltage and current are RMS, or 'root mean square' values):

V_C = IX_C

The voltage across an inductor with reactance X_L (once again, voltage and current are RMS values):

V_L = IX_L

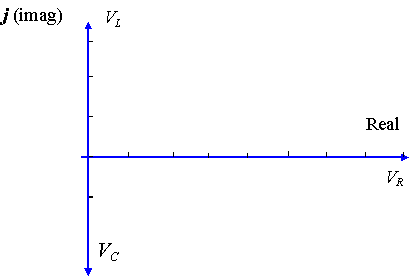
Representing voltages using the complex plane

Using the complex plane, we can represent voltages across resistors, capacitors and inductors.

The voltage across the resistor is regarded as a real quantity, while the voltage across an inductor is regarded as a positive imaginary quantity, and across a capacitor we have a negative imaginary quantity. Our axes are as follows: